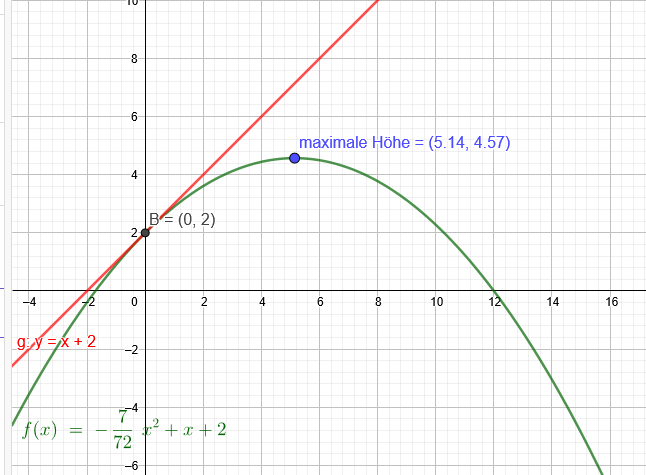
Bei einer Wurfparabel wird die maximale Wurfweite immer bei einem Abwurfwinkel von 45° erreicht. Zudem hängt diese maximale Wurfweite natürlich von der Anfangsgeschwindigkeit der Kugel, also von der Kraft des Sportlers ab. Ein Kugelstoẞer stößt aus einer Höhe von 2m und unter einem Winkel von 45° die Kugel 12m (15m, 18m) weit. Berechnen Sie jeweils die maximale Höhe der Flugbahn.
f(x)=a*x^2+b*x+c
f(0)=c
1.)c=2
f(12)=144a+12b+2
2.)144a+12b+2=0 → 72a+6b+1=0
f´(x)=2ax+b
f´(0)=b
tan(45°)=1
b=1 in 2.) 72a+6+1=0 72a+7=0 a=-\( \frac{7}{72} \)
f(x)=-\( \frac{7}{72} \)x^2+x+2
Maximale Höhe:
f´(x)=-\( \frac{7}{36} \)x+1
-\( \frac{7}{36} \)x+1=0
x=\( \frac{36}{7} \) f(\( \frac{36}{7} \))=-\( \frac{7}{72} \)*(\( \frac{36}{7} \))^2+\( \frac{36}{7} \)+2=\( \frac{32}{7} \)