Aufgabe:
Gegeben sei die Matrixgleichung X⋅A+X⋅B=C mit den Matrizen
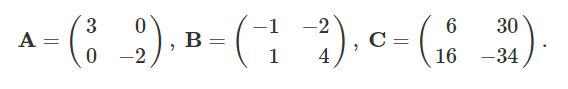
Text erkannt:
\( \mathbf{A}=\left(\begin{array}{rr}3 & 0 \\ 0 & -2\end{array}\right), \mathbf{B}=\left(\begin{array}{rr}-1 & -2 \\ 1 & 4\end{array}\right), \mathbf{C}=\left(\begin{array}{rr}6 & 30 \\ 16 & -34\end{array}\right) \)
Bestimmen Sie die Matrix X und die Determinante von X.
Problem/Ansatz:
Bei meinem Rechenweg scheint ein Fehler drinn zu sein. Ich habe folgendermaßen gerechnet:
Gleichung nach x aufgelöst: x= C*(A+B)^-1
Dann die Matrixen eingesetzt. Für x kam dann die Matrixe:
x=(2, 10, -2,66, -11,33).
Für die Determinante von x habe ich folgendeermaßen gerechnet: (2*(-11,33))- (10*(-2,66))= 3,94
Könnte mir vielleicht jemand sagen wo ich falsch gerechnet habe? Bzw. den Rechenweg/Lösung online stellen? Vielen Dank im Voraus
