Funktionsgleichung mit möglichst niedrigem Grad

Question

Aufgabe:

Es soll eine Funktionsgleichung f(x) mit möglichst niedrigen Grad gefunden werden, welche die folgenden Eigenschaften erfüllt.
Der Graph von f(x) läuft durch den Punkt P(0;-5).
Im Punkt E(-8;3) hat der Graph von f(x) einen Extrempunkt.
x=6 ist eine Wendestelle.
Geben Sie die Gleichung an

Problem/Ansatz:

Hey, an sich weiß ich eigentlich wie man das ausrechnet… aber diese Aufgabe gehört zu einem Test den wir zuhause machen können und der sehr, sehr wichtig für meine Note ist… also wollte ich fragen ob mir das eventuell jemand ausrechnen könnte

Danke schonmal im Voraus LG

Answer 1

DIe Kurznotation der Angaben
f ( 0 ) = -5 Koordinate
f ( -8 ) =3 Koordinate
f ' ( -8 ) = 0  Steigung
f '' ( 6 ) = 0 Wendestelle

4 Angaben = Funktion 3.Grades

f ( x ) = ax^3 + bx^2 + cx + d
f ´( x ) = 3ax^2 + 2bx + c
f ´´( x ) = 6ax + 2b

Einsetzen
f ( 0 ) = a*(0)^3 + b*(0)^2 + c *0 + d = -5
f ( 0 ) = d = -5  => d = -5

f ( x ) = ax^3 + bx^2 + cx -5

Ich hoffe du kannst ein lineares Gleichungs-
sytem aufstellen und berechnen.

Zur Kontrolle
f(x) = 1/272·x^3 - 9/136·x^2 - 30/17·x - 5

Falls nicht dann melde dich wieder.

Answer 2

f(x) = ax^3+bx^2+cx+d

f(0) = -5

f(-8)=3

f '(-8)= 0

f ''(6) =0

Answer 3

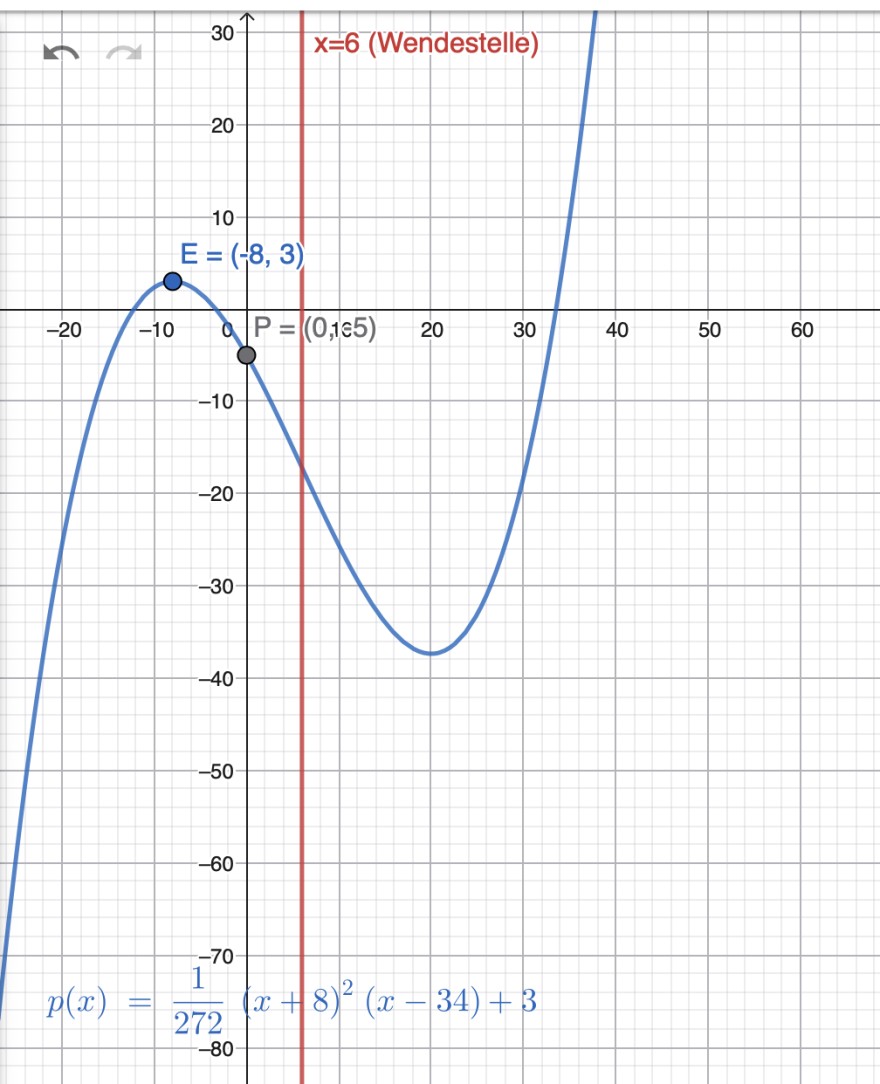
Es soll eine Funktionsgleichung f(x) mit möglichst niedrigen Grad gefunden werden, welche die folgenden Eigenschaften erfüllt.
Der Graph von f(x) läuft durch den Punkt P(0|-5).
Im Punkt E(-8|3) hat der Graph von f(x) einen Extrempunkt.
x=6 ist eine Wendestelle.
Geben Sie die Gleichung an.

Im Punkt E(-8|3) hat der Graph von f(x) einen Extrempunkt: Verschiebung um 3 Einheiten nach unten:

E´(-8|0)

Der Graph hat im Extrempunkt eine zweifache Nullstelle. Linearfaktorenform:  3.Grad wegen Extrempunkt und Wendepunkt.

\(f(x)=a ( x+8)^2(x-N)\\=a(x^2+16x+64)(x-N) \\ =a(x^3+16x^2+64x-Nx^2-16Nx-64N)\)

...x=6 ist eine Wendestelle. 2. Ableitung

\(f'(x)=a(3x^2+32x+64-2Nx-16N)\)

\(f''(x)=a(6x+32-2N)\)   

\(f''(6)=a(36+32-2N)=a(68-2N)=0\)

\(N=34\)

\(f(x)=a ( x+8)^2(x-34)\)

...läuft durch den Punkt P(0|-5)→  P´(0|-8)→

\(f(0)=a ( 8)^2(-34)=-8\)

\(a=\frac{1}{272}\)

\(f(x)=\frac{1}{272} ( x+8)^2(x-34)\)

...um 3 Einheiten nach oben:

\(p(x)=\frac{1}{272} ( x+8)^2(x-34)+3\)