Aufgabe:

Text erkannt:
Aufgabe 3:
(7 Punkte)
Gegeben sei der Bereich
\( A=\{(x, y): x, y>0,0<x y<3, x<y<2 x\} . \)
Skizzieren Sie \( A \) und berechnen Sie mittels der Transformation \( u:=x y \) und \( v=\frac{y}{x} \) das Integral
\( \int \limits_{A} y^{2} d(x, y) \text {. } \)
Problem/Ansatz:
Text erkannt:
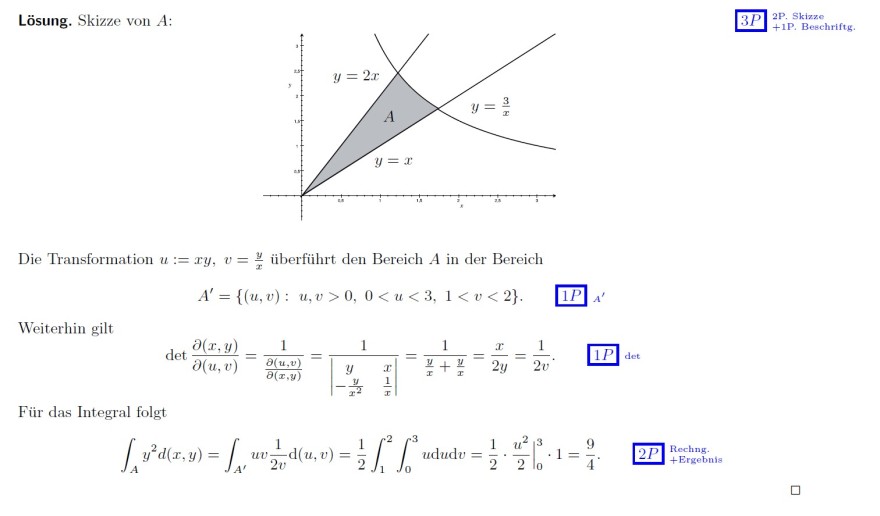
Lösung. Skizze von \( A \) :
Die Transformation \( u:=x y, v=\frac{y}{x} \) überführt den Bereich \( A \) in der Bereich
\( A^{\prime}=\{(u, v): u, v>0,0<u<3,1<v<2\} . \quad 1 P_{A^{\prime}} \)
Weiterhin gilt
\( \operatorname{det} \frac{\partial(x, y)}{\partial(u, v)}=\frac{1}{\frac{\partial(u, v)}{\partial(x, y)}}=\frac{1}{\left|\begin{array}{cc} y & x \\ -\frac{y}{x^{2}} & \frac{1}{x} \end{array}\right|}=\frac{1}{\frac{y}{x}+\frac{y}{x}}=\frac{x}{2 y}=\frac{1}{2 v} . \)
\( 1 P \) det
Für das Integral folgt
\( \int \limits_{A} y^{2} d(x, y)=\int \limits_{A^{\prime}} u v \frac{1}{2 v} \mathrm{~d}(u, v)=\frac{1}{2} \int \limits_{1}^{2} \int \limits_{0}^{3} u \mathrm{~d} u \mathrm{~d} v=\left.\frac{1}{2} \cdot \frac{u^{2}}{2}\right|_{0} ^{3} \cdot 1=\frac{9}{4} . \)
Warum muss man das Oberflächenintegral mit der determinate berechnen? Ich verstehe den rechenweg nicht ganz.