Integration von Wurzelfunktionen

Question

Aufgabe:

Integration von Wurzelfunktionen

Die Aufgabe:

y²=3x

y²=9/2(x-1)

ich habe  3x-(9/2(x-1) berechnet die Grenzen sind 0bis 3

ich habe dann integriert und kommt 6,75 heraus ist aber falsch

Comments

Was ist die eigentliche Aufgabe? Wenn auch x=0 zum irgendwie relevanten Bereich gehören soll, wäre y²=4.5(x-1) nicht erfüllbar??

---

Die Aufgabe:
y²=3x
y²=9/2(x-1)

Das ist keine Aufgabe. Das ist eine Liste von Gleichungen.

---

Berechne den Inhalt eines Flächenstücks, das von den Parabeln mit den Gleichungen y²=3x und y²= 9/2(x-1) begrenzt wird !

---

Es muss doch eine in Worte gefasste Aufgabenstellung geben, etwa "Berechne das Integral...." oder "Berechne die Fläche ..."

Answer 1

Stell dir also einfach die x und y-Achse vertauscht vor.

Dann hast du nur zwei Parabeln.

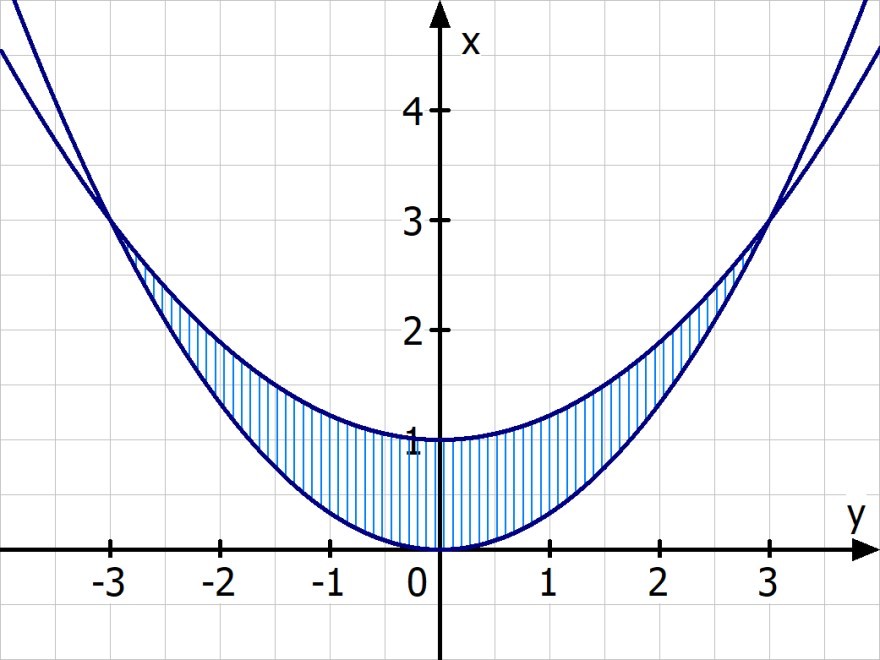
Funktionen der Parabeln aufstellen

y² = 3·x --> x = 1/3·y²

y² = 9/2·(x - 1) --> x = 2/9·y² + 1

Schnittpunkte / bzw. nur y-Koordinate der Schnittpunkte

1/3·y² = 2/9·y² + 1 --> y = -3 ∨ y = 3

Flächenstück

A = ∫ (-3 bis 3) ((2/9·y² + 1) - (1/3·y²)) dy = 4

Answer 2

Hallo,

man kann natürlich die Integrale über den Wurzel-Funktionen berechnen. Man kann aber auch über $y$ integrieren. Umgestellt nach $x$ gibt:$$x= \frac13 y^3;\quad \quad x= \frac29 y^2+1$$Die Schnittpunkte liegen bei $(3;\,\pm3)$. Folglich sind $y=\pm3$ die Integrationsgrenzen für die Berechnung der Fläche $F$

Und die Rechnung vereinfacht sich nun zu$$F=\int\limits_{y=-3}^{3}\left(\frac29y^2+1 -\frac13y^2\right)\,\text dy\\ \phantom{F}= \int\limits_{y=-3}^{3}\left(-\frac19y^2+1\right)\,\text dy\\ \phantom{F}= \left.-\frac1{27}y^3+y\right|_{y=-3}^{3} \\ \phantom{F}= 2-(-2)\\\phantom{F}=4$$Guß Werner

Answer 3

$2\cdot\int_0^3(\sqrt{4.5x-4.5}-\sqrt{3x})dx$

Comments

Diese "Antwort" zu geben, nachdem schon im ersten Kommentar darauf hingewiesen wurde, dass die erste Wurzel im Integrationsbereich nicht (überall) definiert ist, finde ich dreist.

Answer 4

$y^2=3x$

$x=\frac{y^2}{3}$

Umkehrfunktion:   $f(x)=\frac{x^2}{3}$ in rot

$y^2= \frac{9}{2} * (x-1)$

$y^2= \frac{9}{2} *x-\frac{9}{2}$

$\frac{9}{2} *x=y^2+\frac{9}{2}$

$x=\frac{2}{9}*y^2+1$

Umkehrfunktion:   $g(x)=\frac{2}{9}*x^2+1$ in grün

Da die beiden Parabeln zur y-Achse symmetrisch sind, gilt

$A= 2*\int\limits_{0}^{3}(g(x)-f(x))*dx$