Induktion mit Summenzeichen

Question

Aufgabe:

Induktion mit Summenzeichen

Problem/Ansatz:

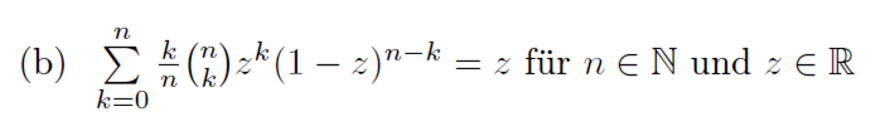
Text erkannt:

(b) $\sum \limits_{k=0}^{n} \frac{k}{n}\left(\begin{array}{l}n \\ k\end{array}\right) z^{k}(1-z)^{n-k}=z$ für $n \in \mathbb{N}$ und $z \in \mathbb{R}$

Ich soll dies mit einer Induktion beweisen. Grundsätzlich habe ich Induktionen verstanden und die anderen Teilaufgaben

auch ohne Probleme geschafft. Allerding komme ich hier auf keinen Ansatz, da mich das n in der Summe verwirrt und auch der Binomialkoeffizient.

Ich würde mich freuen, wenn mir jemand hier weiterhelfen kann,

Vielen Dank schonmal im Voraus :)

Comments

Muss der Beweis notwendigerweise per Induktion erfolgen oder darf es auch ein direkter sein?

Answer 1

Alternativer Beweis ohne Induktion durch Binomischen Satz:

Wie abakus schon bemerkte ist $\frac{k}{n}{n \choose k}={{n-1}\choose {k-1}}$.

Hiermit ergibt sich$$\sum_{k=0}^n\frac{k}{n}{n \choose k}z^k(1-z)^{n-k}=z\cdot \sum_{k=1}^n{{n-1}\choose {k-1}}z^{k-1}(1-z)^{(n-1)-(k-1)}=\\=z\cdot \sum_{l=0}^{n-1}{{n-1}\choose l}z^l(1-z)^{(n-1)-l}=z\cdot (z+(1-z))^{n-1}=z\cdot 1^{n-1}=z$$

Answer 2

$n\choose k$ ist definiert als $\frac{1\cdot 2\cdot 3\cdots \cdot (n-1)\cdot n}{(1\cdot 2\cdot 3\cdots \cdot (k-1)\cdot k)\cdot (1\cdot 2\cdot 3\cdots \cdot (n-k))}$.

mit dem zusätzlichen Faktor $\frac{k}{n}$ kann man in $$\frac{\red{k}}{\blue{n}} \frac{1\cdot 2\cdot 3\cdots \cdot (n-1)\cdot \blue{n}}{(1\cdot 2\cdot 3\cdots \cdot (k-1)\cdot \red{k})\cdot (1\cdot 2\cdot 3\cdots \cdot (n-k))}$$ die Faktoren k und n kürzen, es entsteht $\frac{1\cdot 2\cdot 3\cdots \cdot (n-1)}{(1\cdot 2\cdot 3\cdots \cdot (k-1))\cdot (1\cdot 2\cdot 3\cdots \cdot (n-k))}$

Comments

Heißt ich kann den ersten Teil im IS auf (n über k-1) kürzen?

Und inwiefern bringt mir dies in der Induktion xD

Ich hänge bei der Aufgabe irgendwie komplett im Dunkeln...

---

Heißt ich kann den ersten Teil im IS auf (n über k-1) kürzen?

Im Prinzip ja, aber

Im Zuge der Induktion wird ja aus n dann n+1 gemacht ...

Dann bekommst du im Zähler einen Faktor mehr, und im Nenner kommt ganz hinten auch ein Faktor (n+1-k) hinzu.