Aufgabe:
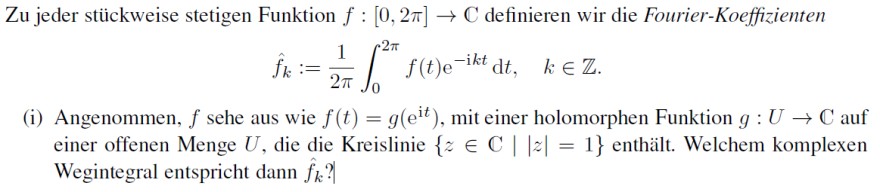
Text erkannt:
Zu jeder stückweise stetigen Funktion \( f:[0,2 \pi] \rightarrow \mathrm{C} \) definieren wir die Fourier-Koeffizienten
\( \hat{f}_{k}:=\frac{1}{2 \pi} \int \limits_{0}^{2 \pi} f(t) \mathrm{e}^{-\mathrm{i} k t} \mathrm{~d} t, \quad k \in \mathbb{Z} . \)
(i) Angenommen, \( f \) sehe aus wie \( f(t)=g\left(\mathrm{e}^{\mathrm{i} t}\right) \), mit einer holomorphen Funktion \( g: U \rightarrow \mathrm{C} \) auf einer offenen Menge \( U \), die die Kreislinie \( \{z \in \mathrm{C}|| z \mid=1\} \) enthält. Welchem komplexen Wegintegral entspricht dann \( \hat{f}_{k} \) ?
Problem/Ansatz:
Ich verstehe leider gar nicht, was ich mit der Information f(t) = g(e^it) anfangen soll.
Also so wie ich es verstanden habe, soll ja am Ende ein Wegintegral γ mit γ = {z : |z| = 1} rauskommen. Aber mir fehlt leider der Ansatz, wie ich dort hin komme.