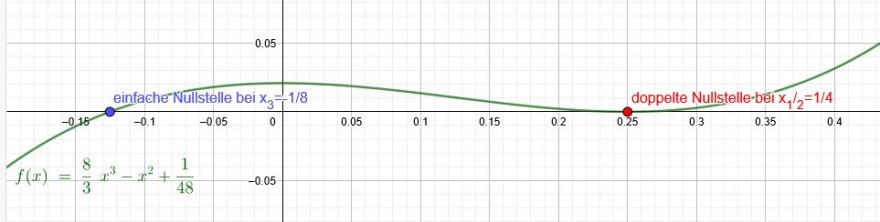
Bei der gegebenen Funktion \(f(x)\) lässt sich \(x^2\) wie gezeigt ausklammern.
Ich verschiebe nun den Graph von \(f(x)\) um \( \frac{1}{48} \) nach oben:
\(p(x)=\frac{8}{3}x^3-x^2+\frac{1}{48}\)
\(\frac{8}{3}x^3-x^2+\frac{1}{48}=0\)
Nun lässt sich \(x^2\) nicht mehr ausklammern. Das führt zu einem anderen Verfahren:
\(p'(x)=8x^2-2x\)
\(8x^2-2x=0\)
\(4x^2-x=0\) → \(x\) ausklammern:
\(x(4x-1)=0\)
Eine Extremstelle ist nun bei \(x_1=0\) → \(p(0)=\frac{1}{48}\)
Eine weitere bei \(x_2=\frac{1}{4}\) → \(p(\frac{1}{4})=\frac{8}{3} \cdot (\frac{1}{4})^3-(\frac{1}{4})^2+\frac{1}{48}=0\)
Hier existiert nun eine doppelte Nullstelle (Extremwert)
Polynomdivision:
\((\frac{8}{3}x^3-x^2+\frac{1}{48}):(x-\frac{1}{4})^2=(\frac{8}{3}x^3-x^2+\frac{1}{48}):(x^2-\frac{1}{2}x+\frac{1}{16})=\frac{8}{3}x+\frac{1}{3}\)
Die 3. Nullstelle liegt nun bei \(x_3=-\frac{1}{8}\) Sie ist einfach.