Aufgabe: Ein Glasgefäß (Wandstärke vernachlässigbar dünn) hat die Form eines Pyramidenstumpfes.
Die Seitenlänge der Grundfläche beträgt 12 cm, diejenige der Deckfläche beträgt 6 cm, die Höhe
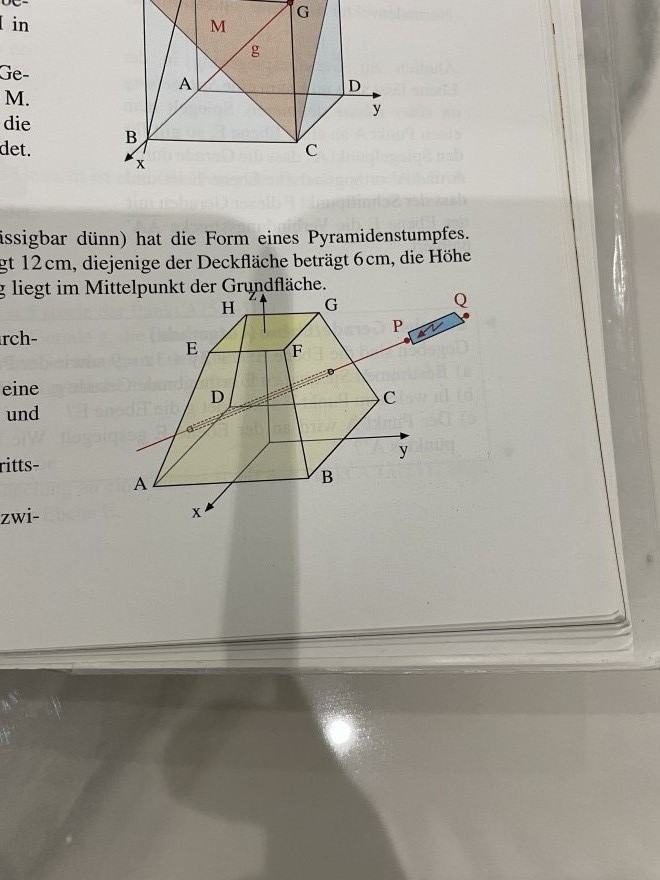
beträgt 6cm. Der Koordinatenursprung liegt im Mittelpunkt der Grundfläche.
Ein Lichtstrahl durch die Punkte P (-10|22|8) und Q (-14|31|10) durchdringt das Gefäß.
a) Bestimmen Sie eine Parameter- und eine
Koordinatenform der Ebenen ADE und
BCG.
b) Berechnen Sie den Ein- und Austritts-
punkt des Lichtstahls.
c) Ermitteln Sie die Länge der Strecke zwi
schen Ein- und Austrittspunkt.
Problem/Ansatz: Wie muss ich das berechnen? Für eine Erklärung wäre ich sehr dankbar.
Lg
Text erkannt:
in
M. die det.
issigbar dünn) hat die Form eines Pyramidenstumpfes. gt \( 12 \mathrm{~cm} \), diejenige der Deckfläche beträgt \( 6 \mathrm{~cm} \), die Höhe liegt im Mittelpunkt der Grundfläche.
Text erkannt:
lünn) hat die Form eines Pyramidenstumpfes. diejenige der Deckfläche beträgt \( 6 \mathrm{~cm} \), die Höhe Mittelpunkt der Grundfläche.