Hier eine Skizze:
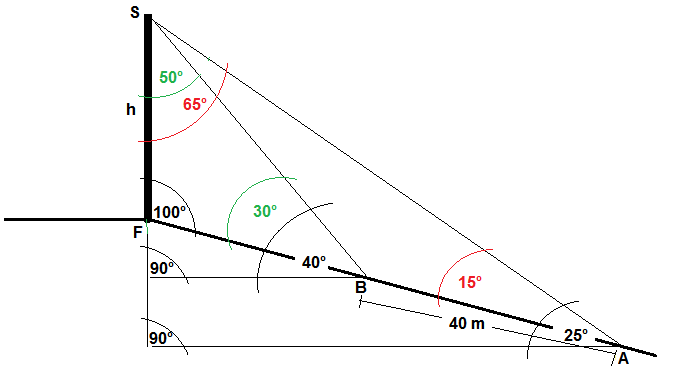
Aus der Skizze ergibt sich mit dem Sinussatz:
$$\frac { h }{ sin(15°) } =\frac { |BF|+40 }{ sin(65°) }$$und$$\frac { h }{ sin(30°) } =\frac { |BF| }{ sin(50°) }$$$$\Leftrightarrow$$$$h=\frac { (|BF|+40)*sin(15°) }{ sin(65°) }$$und$$h=\frac { |BF|*sin(30°) }{ sin(50°) }$$Gleichsetzen:$$\Leftrightarrow \frac { (|BF|+40)*sin(15°) }{ sin(65°) } =\frac { |BF|*sin(30°) }{ sin(50°) }$$Auflösen nach |BF|:$$\Leftrightarrow (|BF|+40)*sin(15°)*sin(50°)=|BF|*sin(30°)*sin(65°)$$$$\Leftrightarrow |BF|*sin(15°)*sin(50°)+40*sin(15°)*sin(50°)=|BF|*sin(30°)*sin(65°)$$$$\Leftrightarrow 40*sin(15°)*sin(50°)=|BF|*sin(30°)*sin(65°)-|BF|*sin(15°)*sin(50°)$$$$\Leftrightarrow 40*sin(15°)*sin(50°)=|BF|*(sin(30°)*sin(65°)-sin(15°)*sin(50°))$$$$\Leftrightarrow |BF|=\frac { 40*sin(15°)*sin(50°) }{ sin(30°)*sin(65°)-sin(15°)*sin(50°) } =31,114m$$Daraus folgt für h (siehe oben):$$\Rightarrow$$$$h=\frac { |BF|*sin(30°) }{ sin(50°) } =\frac { 31,114*sin(30°) }{ sin(50°) } =20,31m$$
EDIT:
Herrje, man kann's wirklich kompliziert machen ... :-)
Einfacher ist es so:
Da der Winkel ASB 65 ° - 50 ° = 15 ° groß ist, ist das Dreieck ASB ein gleichschenkliges Dreieck. Daher ist
| BS | = | BA | = 40 m
und es gilt einfach nach dem Sinussatz:
$$\frac { |BS| }{ sin(100°) } =\frac { h }{ sin(30°) }$$$$\Leftrightarrow \frac { 40 }{ sin(100°) } =\frac { h }{ sin(30°) }$$$$\Leftrightarrow h=\frac { 40*sin(30°) }{ sin(100°) }$$$$\Leftrightarrow h\approx 20,31m$$