Algebraische Strukturen Analyse von einer Gruppe
G = (ℤ*3 X ℤ3 , ⊗)
mit (a,b) ⊗ (c,d) = (a *3 c, b +3 d)
Die Aufgabe soll ich unter verschiedenen Gesichtspunkten analysieren. Ich kenne bereits einige Grundlagen der Algebraischen Strukturen, andere notwendige Verfahren, um die Aufgabe zu lösen, konnte ich noch nicht logisch mit dem bereits Gelernten verknüpfen. Komme leider auch nicht mehr alleine weiter.
Was muss ich mit dieser Information anfangen: (ℤ*3 X ℤ3 , ⊗)?
-Ich glaube, dass ich mir den Zahlenraum der ganzen Zahlen betrachte, außer "0" bei der linken Menge und inklusive "0" bei der rechten Menge. Das ⊗ symbolisiert den Operator, um den es sich handelt. Da nur ein Operator vorhanden ist, handelt es sich schon einmal nicht um ein Ring oder Körper. Die Aufgabe sagt jedoch bereits, dass es sich um eine Gruppe handeln muss.
Frage: Muss ich für die Analyse die Mengen " (ℤ*3 X ℤ3 , ⊗)" miteinander kombinieren? sieht das dann so aus: {1,2} und {0,1,2} und erhalte dann die Menge {0,1,2}? oder bilde ich wegen dem "X" das kartesische Produkt:
{(1,0),(1,1),(1,2),(2,0),(2,1),(2,2)}?
1.Des Weiteren soll untersucht werden, ob es sich um eine Abelsche Gruppe handelt.?
-Wenn ich die Mengen {0,1,2} haben sollte, dann müsste ich überprüfen, ob folgende Kriterien vorliegen:
- Abgeschlossenheit, assoziativität, das neutrale Element, inverse Element und das Kommutativgesetz muss gelten.
Für das inverse Element muss gelten a' * a = e -> jedoch wäre das inverse von z.B. 2 nicht in der Grundmenge der ganzen Zahlen vertreten: 2 * 1/2 = 1 wobei 1/2 kein Element aus ℤ ist.
(a,b) ⊗ (c,d) = (a *3 c, b +3 d)
Bei einer Menge von {0,1,2} wüsste ich nicht, wie alle Variablen (a,b,c,d) genau ein Element aus der Menge zugeordnet bekommen. wie genau überprüfe ich hier, ob eine abelsche Gruppe vorliegt.
2. Des Weiteren wird danach gefragt, wie viele Elemente G hat.
Wenn {0,1,2} = 3?
Wenn {(1,0),(1,1),(1,2),(2,0),(2,1),(2,2)} = 6?
3. Geben Sie das neutrale Element der Gruppe an. Bestimmen sie außerdem zu
jedem Element das Inverse.
für das neutrale Element gilt:
3.1 e= neutrales Element
3.2 a * e = a -> bei der Multiplikation ist die 1 das neutrale Element: 2 * 1 = 2
Da müsste ich die Verknüpfungstabelle erstellen und wo ich eine 1 als neutrales Element erhalte, sehe ich, mit welchen Element ein anderes ein Inverses bildet. Muss ich dann zwei Tabellen erstellen wegen :
3.3 (a,b) ⊗ (c,d) = (a *3 c, b +3 d)? Also für die Multiplikation mod 3 und Addition mod 3?
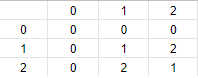
Beispiel für a *3 c aus der Menge {0,1,2}
Text erkannt:
\begin{tabular}{|l|l|l|l|}
\hline & 0 & 1 & 2 \\
\hline 0 & 0 & 0 & 0 \\
\hline 1 & 0 & 1 & 2 \\
\hline 2 & 0 & 2 & 1 \\
\hline
\end{tabular}
Dort würde es für die Null kein Inverses geben und jedoch aber 1' = 1 und 2' = 2.
4. Gibt es eine Untergruppe mit 3 Elementen?
Da die Untergruppe immer eine Teilmenge der Gruppe sein muss, sollte es schon einmal eine Untergruppe von G geben.
Jetzt müsste ich irgendwie schauen, dass ich eine kleinere Menge von der ursprünglichen Menge finde, in denen alle Axiome einer Gruppe weiterhin gelten. Aber wie ich dort vorgehen soll weiß ich leider noch nicht so ganz.
5. Geben Sie eine Untergruppe mit 4 Elementen an.
Dort gilt das selbe wie bei 4). Allerdings könnte es auch sein, dass es eine solche Untergruppe mit 4 Elementen nicht existiert. Wie würde das bei der Aufgabe funktionieren?
6. Die Menge U = {(1,0),(2,0) ist eine Untergruppe von G. Geben Sie die Linksnebenklassen von U an. Ist U ein Normalteiler? Begründen Sie Ihre Antwort.
Stimmt es, dass bei abelschen Gruppen es keinen Unterschied machen würde, wenn ich von links nach rechts oder von rechts nach links multipliziere?
7. Ist G zyklisch, wenn nein Begründen sie warum nicht. Ansonsten geben sie einen Erzeuger an?
Wie überprüfe ich, ob G bei der Multiplikation zyklisch ist?
z.B. wäre bei (ℤ6,⊕) sähe es so aus:
<1> = {1,2,3,4,5,0,1}
<2> = {4,0,2}
<3> = {0,3}
<4> = {2,0,4}
<5> = {4,3,2,1,0,5}
Wenn ich (ℤ3 , ⊗) habe, wären dann die erzeugenden Elemente von {0,1,2} = 1, wegen (1*0=0, 1*1=1, 1*2=2) und 2, wegen (2*0=0, 2*1=2, 2*2= 4 mod 3 = 1).
Wie genau wäre die Lösung für meine ursprüngliche Aufgabe? (ℤ*3 X ℤ 3 , ⊗)?
8. Und als letztes wäre es noch sehr hilfreich zu wissen, wie ich nachweise, dass (ℤ6 , + 6 ) Ein Isomorphismus zu G ist oder nicht. Auch hier ist die frage warum das dann so ist oder eben nicht ist.
Es sind jetzt sehr viele Fragen. Ich hoffe jemand könnte die ein oder andere beantworten. Bestimmt bleibt der ein oder andere "AHA-Moment" nicht aus.
Vielen Dank im Voraus.