Eckpunkte Prisma vektor

Question

Text erkannt:

7. Aufgabe: Sachzusammenhang „Schatten auf der Lagerhalle"
Gegeben ist ein mathematisches Prisma mit den Eckpunkten A, B, C, D, E, F, G und H (siehe Abbildung). Die Grundfläche des Prismas ist ein Trapez. Der Eckpunkt A liegt im Ursprung und die Punkte B, D und E auf den entsprechenden Koordinatenachsen. Die Punkte C, D und $\mathrm{H}$ haben die Koordinaten $C(0|10| 15), D(0|0| 20)$ und $H(30|0| 20)$. Gegeben ist außerdem die folgende Streckenlänge: $\overline{F B} \triangleq 30 L E$
a) Geben Sie die Koordinaten des Eckpunktes $\mathrm{G}$ an.

Aufgabe:

… Was sind die anderen Eckpunkte

Problem/Ansatz:

Answer 1

E(30;0;0)  wegen FB=30

F(30;10;0)   weil C die y-Koo 10 hat

B(0;10;0) dito

G(30;10;15) wegen 3. Koo von C.

Answer 2

Hallo Lukas,

mache Dir ein Bild:

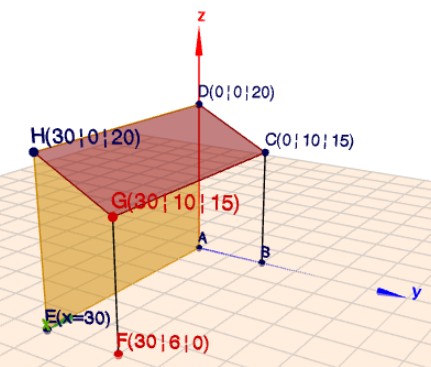
Die Punkte $A$, $C$, $D$ und $H$ sind gegeben. Da $\overline{FB} = 30$ und der Schuppen wohl im Grundriss rechteckig, ist auch $\overline{EA}=30$ und folglich $E=(30|\,0|\,0)$. Somit hat $E$ auch den gleichen XY-Wert wie $H$.

Gleiches gilt für $B$. $C=(0|\,10|\,15)$ daraus fogt $B=(0|\,10|\,0)$. Und $G$ hat den gleichen YZ-Wert wie $C$ und die gleiche X-Koordinate wie $H$. Also $G=(30|\,10|\,15)$.

$F$ hat die gleichen XY-Koordinaten wie $G$ und die Z-Koordinate ist $=0$, genau wie bei $A$, $B$ und $E$.