Weisen sie nach, dass es keinen Wert von k gibt für den genau 2 gemeinsame Punkt existieren.

Question

Aufgabe:

\( f(x)=\frac{2 x^{2}}{x^{2}+2} \quad y = k \cdot x^{2} \)

Der Graph von f und die Parabel \( y=k \cdot x^{2} \) besitzen für jeden Wert von k mindestens einen gemeinsamen Punkt. Weisen sie nach, dass es keinen Wert von k gibt für den genau 2 gemeinsame Punkte existieren.

Problem/Ansatz:

Kann mir jemand bei dieser Aufgabe helfen?

Answer 1

2·x^2/(x^2 + 2) = k·x^2

2·x^2 = k·x^2·(x^2 + 2)

k·x^2·(x^2 + 2) - 2·x^2 = 0

x^2·(k·(x^2 + 2) - 2) = 0

x = 0

k·(x^2 + 2) - 2 = 0 --> x = ±√(2/k - 2)

Damit es nur genau 2 Lösungen geben, müsste der Term 2/k - 2 unter der Wurzel gleich null sein. Das ist für k = 1 der Fall. Die Lösung lautet dann

x = ± √(2/1 - 2) = ± 0

und diese Lösung fällt dann mit der ersten Gefundenen Nullstelle überein, sodass es dann nur eine Nullstelle bei x = 0 gibt.

Comments

x = -x  ⇒  x = 0

---

Wie kommt man von k·(x2 + 2) - 2 = 0 auf x = ±√(2/k - 2) ?

---

Man wendet Rechenbefehle an:

Addition von 2

Division durch k

... und zwei weitere...

Und warum kürst du einen Lösungsweg (der das durchaus verdient hat) als beste Lösung, wenn deine Nachfrage beweist, dass du den Lösungsweg nicht mal komplett nachvollziehen kannst?

Damit soll es für heute genug sein.

---

Welchen Schritt verstehst du denn nicht?

k·(x^2 + 2) - 2 = 0
k·(x^2 + 2) = 2
x^2 + 2 = 2/k
x^2 = 2/k - 2
x = ± √(2/k - 2)

Ich glaube schon, dass du das kannst. Du willst nur nicht, weil es so lange dauert, wenn du es machst.

Den im Ernst ich habe schon mehrfach erklärt, dass ein Rechentool wie Wolframalpha oder Photomath hilft solch einfache Gleichungen zu lösen.

---

k·(x2 + 2) - 2 = 0
k·(x2 + 2) = 2
x2 + 2 = 2/k
x2 = 2/k - 2
x = ± √(2/k - 2)

Du willst nur nicht, weil es so lange dauert, wenn du es machst.

Falsch, ich frage, weil ich auf ein anderes Ergebnis komme:

k·(x2 + 2) - 2 = 0
kx²+2k-2 = 0
kx² = -2k+2
x² = (-2k+2)/k
x = ± √(-2k+2)/k

Und gut, wenn du schon von Rechentools sprichst,

Wolframalpha

kommt ebenfalls auf ein anderes Ergebnis:

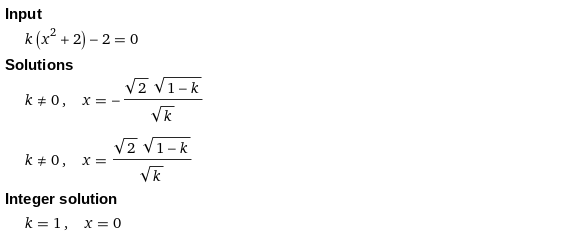
Und ich glaube du möchtest einfach nicht, dass man bei dir nachfragt, weil du Angst hast, dass ein möglicher Fehler, den du gemacht hast, aufgedeckt werden könnte.

---

Welchen Fehler meinst du, den ich gemacht haben könnte.

Wie gesagt, auch ich bin nicht unfehlbar und mache auch viele Fehler. Darum melde mir ruhig einen vermeintlichen Fehler. Wir können gerne darüber diskutieren.

Du weißt das man die drei Wurzeln zu einer Zusammenfassen kann oder nicht ?

$$\frac{\sqrt{2} \cdot \sqrt{1-k}}{\sqrt{k}} \newline \sqrt{\frac{2 \cdot(1-k)}{k}} \newline \sqrt{\frac{2 - 2k}{k}} \newline \sqrt{\frac{2}{k} - 2}$$

---

@Hikoba

Jeder blamiert sich so gut er kann. "Dein" (besser: Der Wolframalpha-) Term

ist identisch mit

 \( \sqrt{\frac{-2k+2}{k}} \)

aus der Antwort vom Mathecoach. Aber sei nicht traurig. Das lernst du noch wenn du groß bist und irgendwann mal Wurzelgesetze und sonstige Umformungsregeln lernst (könnte irgendwann in Klasse 9 oder früher passieren).

Und die wolframalpha-"Integer solution" erhält man auch mit der Formel von Coach, wenn man konkret k=1 einsetzt.

Und entschuldige bitte, dass ich mein Versprechen

Damit soll es für heute genug sein

gebrochen habe. Aber wer so flehend den Ohrfeigenbaum schüttelt, hat auch die Früchte verdient.

---

Hikoba, wenn du deine Lösung umformst

\(x=\pm\sqrt{\frac{-2k+2}{k}}=\pm\sqrt{\frac{-2\cancel{k}}{\cancel{k}}+\frac{2}{k}}=\pm\sqrt{-2+\frac{2}{k}}=\pm\sqrt{\frac{2}{k}-2}\)

sieht sie der vom Mathecoach ziemlich ähnlich, findest du nicht?

Also schau erstmal genau hin, bevor du jemanden beschuldigst, er wolle seine Fehler kaschieren.

Answer 2

Ja. Setze beide Terme \(\frac{2 x^{2}}{x^{2}+2} \) und \(k \cdot x^{2} \) gleich und löse diese Gleichung nach x auf.

Die Substitution z=x² wird dir dabei helfen.

Zähle die so (in Abhängigkeit von k erhaltenen) Lösungen. Sind es irgendwann mal genau 2?

Im Übrigen sind beide Funktionsgraphen symmetrisch zur y-Achse, weswegen alle vom Urspung verschiedenen Schnittpunkte ebenfalls einen der übrigen Schnittpunkte als Spiegelpunkt besitzen.

Ist die Sache damit geklärt?

(Oder soll ich ruhig sein, weil ich wieder mal keine Ahnung davon habe?)

Comments

$$0 = \frac{2x^2}{x^2+2}: kx^2 \\ 0 = \frac{2x^2}{x^2+2}\cdot \frac{1}{kx^2} \\ 0 = \frac{2x^2}{kx^4+2kx^2} \\ 0 = \frac{2z}{kz^2+2kz}$$

Wie genau löst man diese Gleichung jetzt nach x auf?

---

Ein Bruch ist 0, wenn sein Zähler 0 ist (was nur für x=0 der Fall wäre) und sein Nenner nicht 0 ist. Aber dein nenner ist dann auch 0.

Dieser Bruch wird also niemals 0.

Aber das ist nicht schlimm, weil diese Gleichung sowieso nicht zur Aufgabe passt.

---

Ist die Sache damit geklärt?

Das wäre schön, wenn nach einem innerhalb von 3 Minuten geschriebenen Kommentar die Sache geklärt ist.

Wenn die Sache geklärt ist, werde ich das schon in irgendeiner Form signalisieren.

Oder soll ich ruhig sein, weil ich wieder mal keine Ahnung davon habe?

Das traf ja bis jetzt erstmal nur auf die Wahrscheinlichkeitsrechnung zu, aber wenn ich mir den Kommentar von Mathecoach ansehe, sehe ich jetzt weit und breit nichts von einer Substitution...

---

Ja, sicher. Man kann das auch ohne Substitution lösen.

Ich hatte aufgrunde deiner Forums-Vorgeschichte aber die Vermutung, dass du diesen Weg leider nicht hinbekommst. Ich hielt es allerdings für möglich, dass du zumindest eine sich aus der Substitution ergebende einfache quadratische Gleichung lösen kannst. Bei dem Rest (Rücksubstitution und Interpretierung der Ergebnisse) hätte ich dir dann schon geholfen.

---

Seht ihr denn alle nicht, dass beide Funktionen y-achsensymmetrisch sind ?

---

Ich gehöre NICHT zu "alle":

Im Übrigen sind beide Funktionsgraphen symmetrisch zur y-Achse,