Berechnen Sie die Fläche zwischen den Graphen beider Funktionen zwischen den Schnittpunkten.

Question

Aufgabe:

geg: f(x) = x² und g(x) = ax³; a ∈ [1;2]

Berechnen Sie die Fläche zwischen den Graphen beider Funktionen zwischen den Schnittpunkten.

Problem/Ansatz:

Zunächst habe ich die zweite Schnittstelle berechnet:$$f(x)=g(x)\\x^2=ax^3|:x^2\\1=ax|:a\\x=\frac{1}{a}$$Die erste Schnittstelle liegt bei x = 0.

Als nächstes habe ich die obere Funktion identifiziert, durch Einsetzen von a = 1.5 und x = 1:

x² = x² -> 1
ax³ = 1.5x³ -> 1.5

obere Funktion = ax³
untere Funktion = x²

$$\Large\int_{0}^{\frac{1}{a}}g(x)-f(x)\,dx\\\int_{0}^{\frac{1}{a}}ax^3-x^2\,dx\\\left[\frac{ax^3}{4}-\frac{x^2}{3}\right]^\frac{1}{a}_0\\\frac{a\frac{1}{a}^3}{4}-\frac{\frac{1}{a}^2}{3}\\\frac{a\frac{1}{a^3}}{4}-\frac{\frac{1}{a^2}}{3}\\\frac{\frac{a}{a^3}}{4}-\frac{\frac{1}{a^2}}{3}\\\frac{\frac{3a}{a^3}}{12}-\frac{\frac{4}{a^2}}{12}\\\frac{\frac{3a}{a^3}-\frac{4}{a^2}}{12}$$Wenn man jetzt 1.5 einsetzt bekommt man: (3*1.5/1.5^3-4/1.5^2)/12 = -0.037

und das kann nicht sein, denn es soll 3.33 rauskommen:

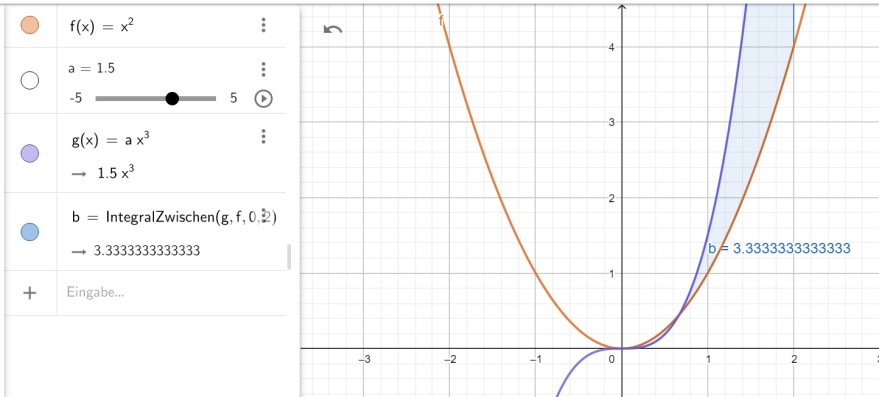
Warum kommt bei mir eine Fläche von -0.037 raus? Wo ist der Fehler?

Comments

und das kann nicht sein, denn es soll 3.33 rauskommen:

Sicher nicht! Du hast mit Geogebra das Integral von 0 bis 2 berechnet. Du brauchst doch bloß den Graphen und die Fläche anzuschauen und dann Deine eigene Überschrift durch zu lesen, dann müsste man doch sehen dass dies falsch ist!

---

Auf ein Bild schauen kann jeder... Sie konnten mir aber nicht sagen, warum bei mir -0.037 rauskommt und nicht -0.025. Darum geht es mir! Wo liegt der Fehler in meiner Rechnung?

---

$$\int_{0}^{\frac{1}{a}}ax^3-x^2\,dx\\\left[\frac{ax^3}{4}-\frac{x^2}{3}\right]^\frac{1}{a}_0\\$$

Das ist falsch. Hier wurde der Exponent nicht um 1 erhöht. Richtig ist $$\dots = \left[\frac{ax^{\color{red}4}}{4} - \frac{x^{\color{red}3}}{3} \right]_0^{1/a} = \frac{1}{a^3} \left(\frac 14 -\frac 13\right) = -\frac{1}{12 a^3}$$ und für $a=1,5=3/2$ wären das dann$$F= -\frac{2^3}{12 \cdot 3^3} = -\frac{2}{81} \approx -0,025$$

Auf ein Bild schauen kann jeder...

drauf schauen ja - aber richtig interpretieren?

Tipp: Die Fläche vor(!) der Rechnung immer schätzen. Und sie ist hier augenscheinlich deutlich kleiner als $1/10$!

---

Bem.: da es hier nur um die Fläche und nicht um das Vorzeichen geht, wäre hier $$F = \int f(x)-g(x)\,\text dx$$ angebracht.

---

Wenn er die obere Funktion nicht auch falsch bestimmt hätte

Als nächstes habe ich die obere Funktion identifiziert, durch Einsetzen von a = 1.5 und x = 1

hätte er die Differenz bestimmt auch richtig aufgeschrieben.

Aber man kann auch einfach sagen man berechnet die gerichtete Fläche von der man am Ende einfach nur den Betrag nimmt.

---

Als nächstes habe ich die obere Funktion identifiziert, durch Einsetzen von a = 1.5 und x = 1:

Jetzt habe ich den Satz auch verstanden ('obere Funktion'!). Danke für den Hinweis. Es wäre dabei so einfach gewesen schlicht auf den Graphen zu schauen, wenn man schon Geogebra & Co zur Verfügung hat.

Unsereiner musste noch mühsam Wertetabellen aufstellen und auf's Papier übertragen. Und trotzdem war das immer die erste Handlung und danach wurde erst gerechnet!

Answer 1

Berechnen Sie die Fläche zwischen den Graphen beider Funktionen zwischen den Schnittpunkten.

d(x) = a·x³ - x² = x²·(a·x - 1) = 0 → x = 0 ∨ x = 1/a
D(x) = a/4·x⁴ - 1/3·x³

Gerichtete Fläche
∫ (0 bis 1/a) d(x) dx = D(1/a) - D(0) = D(1/a) = a/4·(1/a)⁴ - 1/3·(1/a)³ = - 1/(12·a³)

Die Fläche beträgt 1/(12·a³) FE (Flächeneinheiten).

Für a = 1.5 ist die Fläche also 2/81 = 0.02469 groß.

Skizze

Comments

Wie würde man die Werte von a berechnen, für die diese Fläche extremal wird?

Es werden sicherlich 2 Werte rauskommen.

---

Du hast doch a bereits mit 2 vorgegeben. Mir ist nicht klar, was du möchtest. Möchtest du eine obere Integrationsgrenze bestimmen? Dann musst du bis zur Schnittstelle (0.5) integrieren.

---

Wenn du möchtest, dass die von mir bestimmte Fläche (A = 1/(12a³)) extremal wird, muss a den Wert 1 haben. Dann ist die Fläche mit A = 1/12 am größten

---

Wie stellt man bei Geogebra den Schnittpunkt als Grenze ein?

---

Wie stellt man bei Geogebra den Schnittpunkt als Grenze ein?

Die obere Grenze ist 1/a, die du berechnet hast. Und die gibst du auch so ein.

---

Wenn du möchtest, dass die von mir bestimmte Fläche (A = 1/(12a3)) extremal wird, muss a den Wert 1 haben.

Wie würde man das rechnerisch bestimmen?

---

Du solltest wissen das y = 1/x³ für x > 0 streng monoton fallen ist.

D.h. im Intervall [1 ; 2] nimmt die Funktion bei 1 den größten und bei 2 den kleinsten Wert an.

Natürlich kann man auch Monotonie oder Extrempunkte mit der ersten Ableitung bestimmen.

Beachte aber, dass es nur um ein Intervall geht und nicht um alle möglichen Werte von a.

Answer 2

die obere Funktion identifiziert, durch Einsetzen von a = 1.5 und x = 1:

Bei Wahl von a = 1.5 liegt x = 1 außerhalb des Bereiches über den du integrierst.

Außerdem brauchst du dir die Mühe nicht zu machen. Berechne stattdessen

        $\left|\int\limits_0^\frac{1}{a}\left(f(x)-g(x)\right)\mathrm{d}x\right|$.

$\left[\frac{ax^3}{4}-\frac{x^2}{3}\right]^\frac{1}{a}_0$

Die Stammfunktion ist falsch.