Die Punkte durch Funktionsgleichung finden?

Question

Aufgabe:

Parabel und Funktionsgleichung

Problem/Ansatz: ich kann die Aufgaben nicht lösen, habe morgen Klausur.

Text erkannt:

4
Eine parabelförmige Brücke wird durch die Funktion f mit $f(x)=-0,004 x^{2}+1,2 x-32,4$ beschrieben. Die durch die Punkte $\mathrm{A}$ und $\mathrm{B}$ verlaufende Straße liegt auf der $\mathrm{x}$-Achse. Der Verankerungspunkt $\mathrm{C}$ liegt auf der $\mathrm{y}$-Achse.
a) Berechnen Sie die Länge der Straße zwischen den Punkten A und B.
b) Wie tief unter der Straße befinden sich die Verankerungspunkte C und D?
c) Ermitteln Sie die Funktionsgleichung der Träger durch $\mathrm{C}$ und $\mathrm{S}$ bzw. durch $\mathrm{D}$ und $\mathrm{S}$.

Comments

Da bist du ja zeitig dran.

Answer 1

Hallo,

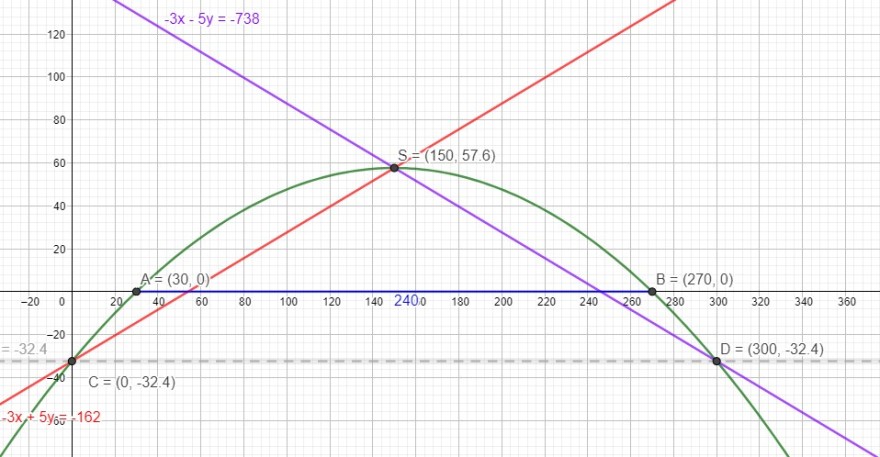
a) A und B sind die Nullstellen der Funktion. Löse also $-0,004x^2+1,2x-32,4=0$ nach x auf.

Die Differenz deiner Ergebniss entspricht der Länge der Strecken zwischen A und B.

b) C ist Schnittpunkt der Funktion mit der y-Achse, den du an der Funktionsgleichung ablesen kannst. Oder setze 0 für x ein.

c) S ist der Scheitelpunkt der Parabel bzw. ihr Hochpunkt.

Die Koordinaten von S bestimmst du, indem du f(x) in die Scheitelpunktform umwandelst.

Die Träger durch C und S bzw. D und S sind Geraden, deren allgemeine Gleichung y = mx + b lautet. Du weißt, dass D die gleiche y-Koordinate wie C hat. Mit dieser Information kannst du die y-Koordinate berechnen, wenn du f(x) = - 32,4 setzt.

Weißt du, wie man eine Geradengleichung aufstellt, wenn zwei Punkte bekannt sind?

Gruß, Silvia

Comments

Herzlichen Dank und liebe Grüße

Roza