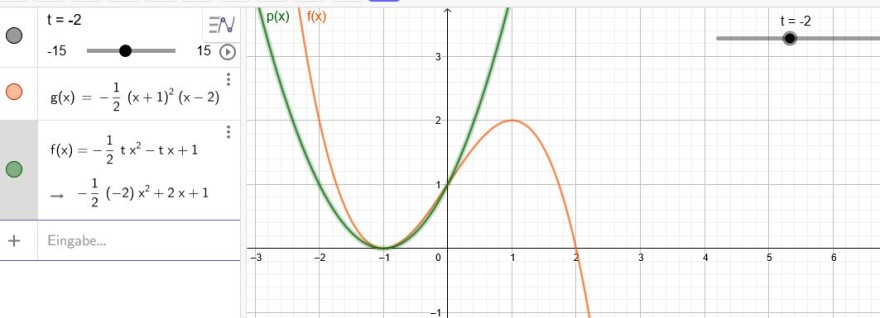
Für welche t berührt das Schaubild der Parabel p mit der Gleichung p(x)= -0,5tx²-tx+1 den Graphen der Funktion f mit der Gleichung f(x)= -0,5(x+1)²(x-2) (Ich wähle t, damit nicht mit m verwechselt wird)
\(p(x)= -\frac{1}{2}tx²-tx+1\)
Umformung in die Scheitelpunktsform der Parabel
\(p(x)= -\frac{1}{2}tx²-tx+1 |*(-2)\)
\(-2*p(x)=tx²+2tx-2 |:t\)
\(-\frac{2}{t}*p(x)=x²+2x-\frac{2}{t} |+\frac{2}{t}\)
\(-\frac{2}{t}*p(x)+\frac{2}{t}=x²+2x |+1\)
\(-\frac{2}{t}*p(x)+\frac{2}{t}+1=x²+2x+1\)
\(-\frac{2}{t}*p(x)+\frac{2}{t}+1=(x+1)^2|*(-\frac{t}{2})\)
\(p(x)+\frac{2}{t}*(-\frac{t}{2})-\frac{t}{2}=(-\frac{t}{2})*(x+1)^2\)
\(p(x)-1-\frac{t}{2}=(-\frac{t}{2})*(x+1)^2\)
\(p(x)=(-\frac{t}{2})*(x+1)^2+1+\frac{t}{2}\) mit \(y_S=1+\frac{t}{2}\) \(1+\frac{t}{2}=0\) →\(t=-2\)
\(f(x)= -0,5*(x+1)^2*(x-2)\) hat eine doppelte Nullstelle bei \(x=-1\) mit waagerechter Tangente
\(p(x)=(x+1)^2\) ist nun die Parabel, die \(f(x)\) in \(x=-1\) berührt.