Zeigen Sie: \operatorname{det}(Cn)=n !.

Question

Aufgabe:

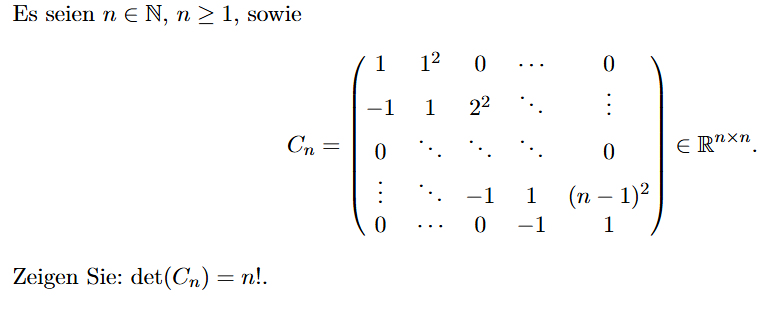
Text erkannt:

Es seien $n \in \mathbb{N}, n \geq 1$, sowie
$C_{n}=\left(\begin{array}{ccccc} 1 & 1^{2} & 0 & \cdots & 0 \\ -1 & 1 & 2^{2} & \ddots & \vdots \\ 0 & \ddots & \ddots & \ddots & 0 \\ \vdots & \ddots & -1 & 1 & (n-1)^{2} \\ 0 & \cdots & 0 & -1 & 1 \end{array}\right) \in \mathbb{R}^{n \times n}$
Zeigen Sie: $\operatorname{det}\left(C_{n}\right)=n$ !.

Problem/Ansatz:

Ich habe das versucht über Induktion und die Streichmatrix zu machen allerdings geht das hier maßlos schief außer ich übersehe etwas. Wäre über Hilfe/Lösung dankbar!

Comments

Nach meinen Berechnungen liefert Entwicklung nach der letzten Zeile
$\det(C_n)=\det(C_{n-1})+(n-1)^2{\cdot}\det(C_{n-2})$.

---

ah ich hab das nach der ersten gemacht. aber das müsste doch eigentlich auch gehen oder nicht?

---

Entwicklung nach der ersten Zeile bringt vermutlich nicht viel, da die dabei entstehenden Streichmatrizen nicht mehr die Form der Matrizen $C_n$ haben. Wenn nach der letzten Zeile entwickelt wird, findet man relativ bald die Matrizen $C_{n-1}$ und $C_{n-2}$ wieder.