Hilfe bei Analysis :)

Question

Aufgabe: ökonischem Definitionsbereich bestimmen, Grenzkosten und Betriebsminimun, Gewinnschwelle- und Grenze sowie Gewinnmaximum und Cournotischer Punkt berechnen

Problem/Ansatz:

Morgen schreiben wir Mathevorklausur und das ist eine Übungsaufgabe und ich hab das solange nicht mehr gemacht, ich versteh garnix.

Gegeben hab wir:

K(x)= x³ -9x² +30x +10

Pn(x)= 42 -6x

Ausgerechnet hab ich schon:

E(x)= -6x² +42x

G(x)= -x³ -15x² +72x +10

Alles danach blick ich nicht mehr durch.

Comments

Das ist echt hinterhältig von den Lehrern, dass die einen immer am Sonntag nachmittags per WhatsApp mit der Nachricht überraschen, dass am Montag Klausur ist.

Answer 1

Der ökonischem Definitionsbereich ist der Bereich in dem Preis und abgesetzte Menge nicht negativ sind. Grenzen sind also 0 und die Nullstelle der Preis-Absatz-Funktion.

Die Grenzkosten sind die Ableitung der Kostenfunktion.

Das Betriebsminimum ist das Minimum der Grenzkostenfunktion. Bestimme also den Tiefpunkt der Grenzkostenfunktion.

Gewinnschwelle und -grenze sind Nullstellen der Gewinnfunktion.

Gewinnmaximum ist die y-Koordinate des Hochpunkts der Gewinnfunktion.

Der cournotsche Punkt ist der Punkt auf der Preis-Absatz-Funktion, bei dem die Gewinnfunktion den Hochpunkt hat.

Answer 2

D = [0;oo)

GK = K'(x)

BM: G'(x) = 0

Gewinnschwelle/-grenze: G(x)= 0

G(x)= E(x)-K(x) = p(x)*x -K(x)

Gewinn-Max: G'(x)= 0

CP:

https://welt-der-bwl.de/Cournotscher-Punkt

Comments

Dankeschön, wo ich jetzt dran hänge ist die Gewinnzone..., ich bekomme 2 negative Zahlen raus. Das kann ja nicht sein oder?

Answer 3

Hallo,

$K(x)=x^3-9x^2+30x+10\\ P_N(x)=42-6x\\ E(x)=42x-6x^2\\ G(x)=-x^3+3x^2+12x-10\\$

ökonischem Definitionsbereich:

Am Graphen der Nachfragefunktion erkennst du, dass Werte außerhalb des Bereichs zwischen 0 und 7 ME entweder eine negative Nachfragemenge oder einen negativen Preis bedeuten würde. Daher liegt der ökonomische Definitionsbereich dazwischen. $D_{ök}=[0;7]$

Grenzkosten

Die Ableitung der Kostenfunktion ist die Grenzkostenfunktion. Ist eine Mengenangabe gegeben, für die du die Grenzkosten berechnen sollst? Dann setze diesen Wert für x in K'(x) ein.

Betriebsminimum

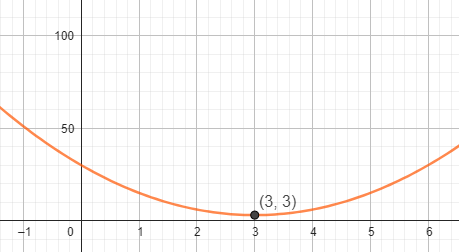
Berechne mit Hilfe der 1. Ableitung das Minimum der Grenzkostenfunktion.

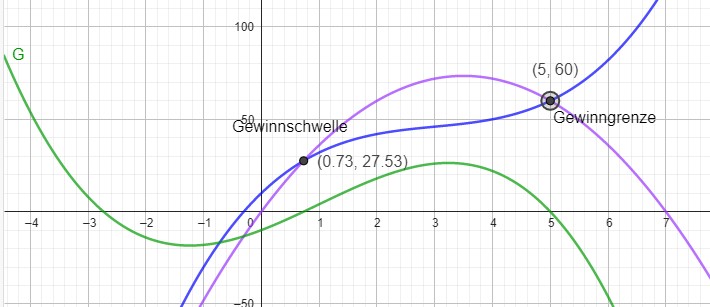
Gewinnschwelle und -grenze sind die Schnittpunkte von E(x) und K(x) bzw. die Nullstellen der Gewinnfunktion.

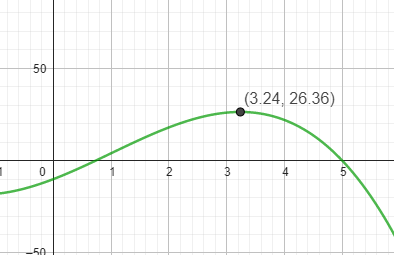
Der gewinnmaximale Produktionspunkt (Hochpunkt von G) gibt an, bei welcher Menge = x der Gewinn = y maximal ist.

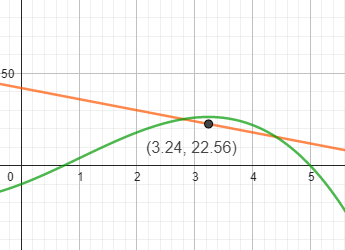
Cournotscher Punkt

Setze den x-Wert des Hochpunkts von G in p ein.

Gruß, Silvia