Wieso kommt das "c" vor die Klammer und weshalb verschwindet es nicht aus der Klammer?

Question

Hallo zusammen,

heute hätte ich direkt mal mehrere Fragen:

1) Wieso kommt das "c" vor die Klammer und weshalb verschwindet es nicht aus der Klammer?

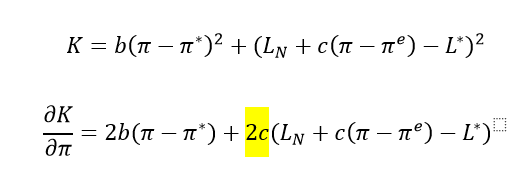
Text erkannt:

$K=b\left(\pi-\pi^{*}\right)^{2}+\left(L_{N}+c\left(\pi-\pi^{e}\right)-L^{*}\right)^{2}$
$\frac{\partial K}{\partial \pi}=2 b\left(\pi-\pi^{*}\right)+2 c\left(L_{N}+c\left(\pi-\pi^{e}\right)-L^{*}\right)$

 2) Wieso dreht sich das (Ln - L*) um zu (L* - Ln)? Und weshalb bleiben bπ* und c² erhalten, obwohl durch b und c² geteilt wird?

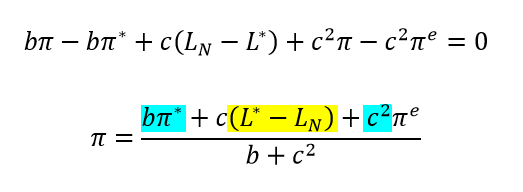
Text erkannt:

$\begin{array}{c}b \pi-b \pi^{*}+c\left(L_{N}-L^{*}\right)+c^{2} \pi-c^{2} \pi^{e}=0 \\ \pi=\frac{b \pi^{*}+c\left(L^{*}-L_{N}\right)+c^{2} \pi^{e}}{b+c^{2}}\end{array}$

Besten Dank vorab und einen schönen Sonntag.

Daniel

Answer 1

Wieso kommt das "c" vor die Klammer

Kettenregel

und weshalb verschwindet es nicht aus der Klammer?

Kettenregel

Wieso dreht sich das (Ln - L*) um zu (L* - Ln)?

Löse die Gleichung nach $\pi$. Sag bescheid wo deine Lösung von der Musterlösung abweicht.

obwohl durch b und c² geteilt wird

Es wird nicht duch b und c² geteilt. Es wird durch b+c² geteilt.

Comments

+c(Ln - L*) würde ich auf die andere Seite der Gleichung holen. Das wäre dann -c(Ln -L*) oder? Ich kann mir nicht erklären wie daraus dann das besagte +c(L* - Ln) wird...

---

Vergleiche mal

      $-2\cdot(5-3)$

und

      $2\cdot(3-5)$.

---

Vielen Dank! Da kam nun der "Aha-Effekt" bei mir :D

Gibt es einen Namen für dieses "Gesetz"?

---

Das ist so trivial, dass es dafür keinen Namen gibt.

Answer 2

Guten Abend. Zur ersten Frage: $c$ ist die innere Ableitung des zweiten Summanden.