Welches Flächenverhältnis haben die beiden Quadrate?

Question

Eine Raute sei in zwei gleichseitige Dreieck zerlegbar. In jedes der beiden Dreiecke wird ein zur längeren Rautendiagonale symmetrisches Quadrat einbeschrieben. Das eine liegt mit allen Eckpunkten auf Dreiecksseiten, das andere nur mit drei Eckpunkten.

Welches Flächenverhältnis haben die beiden Quadrate?

Answer 1

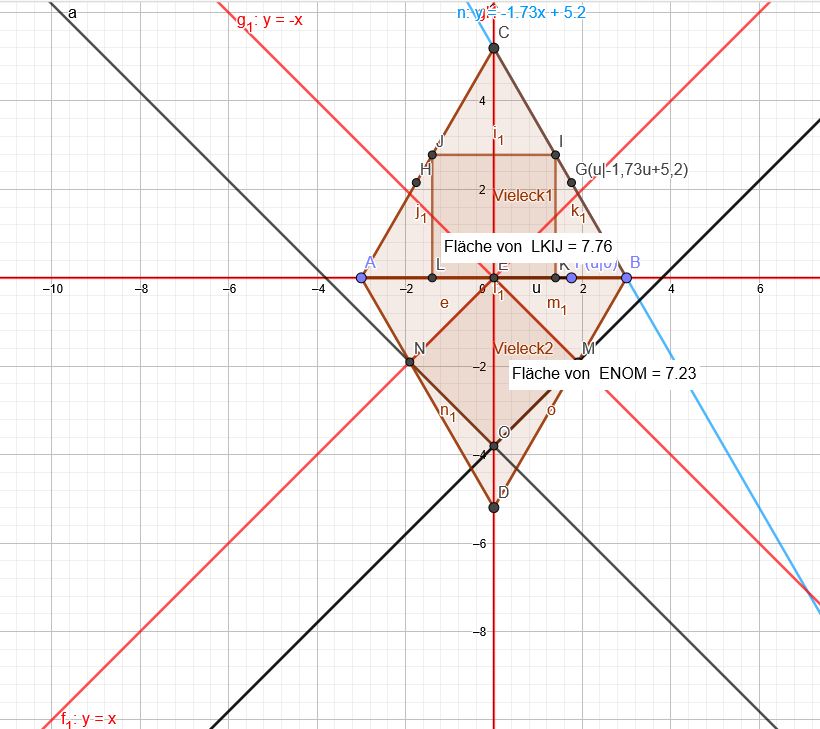
$2u=-1,73u+5,2$    →$u≈1,3941$

Fläche des oberen Quadrats (L,K,I,J): $7,76FE$

Fläche des unteren Quadrats (E,N,O,M): $7,23FE$

Flächenverhältnis: (unteres Quadrat zum oberem Quadrat)$\frac{7,23FE}{7,76FE}≈0,932$   → 93,17%

Vorüberlegung und Lösung:

Comments

Stelle dein Programm auf höhere Genauigkeit ein und vergleiche dann mit dem exakten Wert (2+√3)/4 .

---

Bitte keine Ergebnisse in gerundeten Dezimalbrüchen. Das lässt sich auch exakt darstellen.

---

Flächeninhalt oberes Quadrat:
$B(3|0)$    $tan (120°)=- \sqrt{3}$
Gerade durch $B(3|0)$ :
$y =- \sqrt{3}*x+3*\sqrt{3}$    $x=u$
$y =- \sqrt{3}*u+3*\sqrt{3}$ 
$2u =- \sqrt{3}*u+3*\sqrt{3}$
$2u + \sqrt{3}*u=3*\sqrt{3}$
$u*(2 + \sqrt{3})=3*\sqrt{3}$
$u=\frac{3*\sqrt{3}}{(2 + \sqrt{3})}$
Flächeninhalt oberes Quadrat: $A_1=2*\frac{3*\sqrt{3}}{(2 + \sqrt{3})}*2*\frac{3*\sqrt{3}}{(2 + \sqrt{3})}$
$A_1=\frac{108}{7+4*\sqrt{3}}$
Flächeninhalt unteres Quadrat:
Gerade durch $B(3|0)$ :
$y = \sqrt{3}*x-3*\sqrt{3}$  geschnitten mit $y=-x$:
$\sqrt{3}*x-3*\sqrt{3}=-x$
$\sqrt{3}*x+x=3*\sqrt{3}$
$x*(\sqrt{3}+1)=3*\sqrt{3}$
$x=\frac{3*\sqrt{3}}{1+\sqrt{3}}$    $y=-\frac{3*\sqrt{3}}{1+\sqrt{3}}$
$s^2=x^2+y^2=(\frac{3*\sqrt{3}}{1+\sqrt{3}})^2+(\frac{(-3)*\sqrt{3}}{1+\sqrt{3}})^2=2*(\frac{3*\sqrt{3}}{1+\sqrt{3}})^2$

Zwischenrechnung:

$(\frac{3*\sqrt{3}}{1+\sqrt{3}})^2=\frac{27}{4+2*\sqrt{3}}$ 

----

$A_2=2*(\frac{3*\sqrt{3}}{1+\sqrt{3}})^2=2*\frac{27}{4+2*\sqrt{3}}=\frac{27}{2+\sqrt{3}}$

Flächenverhältnis: (unteres Quadrat zum oberem Quadrat)

$\frac{A_2}{A_1}=\frac{\frac{27}{2+\sqrt{3}}}{\frac{108}{7+4*\sqrt{3}}}=\frac{7+4*\sqrt{3}}{8+4*\sqrt{3}}$

---

Berechne dies neue Ergebnis mal mit den Taschenrechner und vergleiche es mit deinem Ergebnis von oben.

---

Endlich! Jetzt dürfte es richtig sein.

---

Ja, jetzt ist es richtig. Man könne allerdings auch noch den Nenner rational machen. Deine zunächst angegebene dritte Nachkommastelle war um 1 zu niedrig. Wer im Laufe der Rechnung bereits mit gerundeten Werten weiterrechnet, ist nie vor solchen Fehlern sicher.