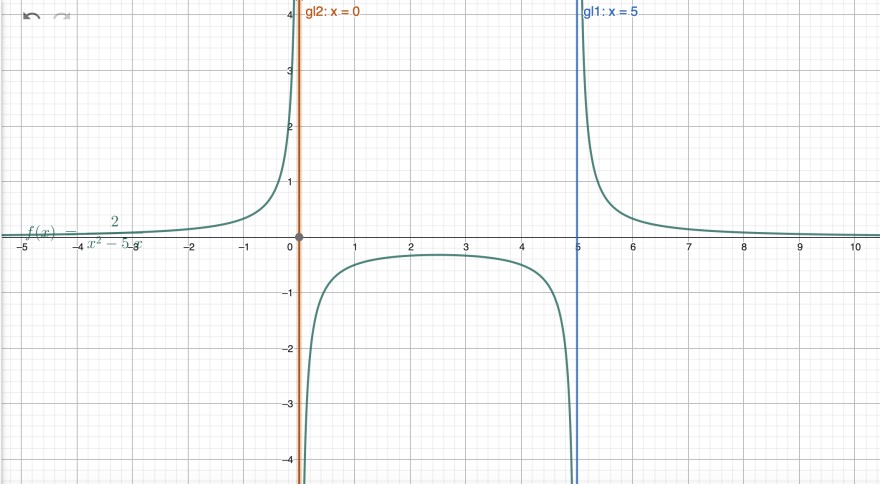
\(f(x)=\frac{2}{x^2-5x}\)
Zum Finden der Definitionslücken muss der Nenner = 0 sein:
\(x^2-5x=0\).
\(x(x-5)=0 \) Satz vom Nullprodukt:
\(x_1=0 \) oder \(x_2=5\)
Bei der Beispielaufgabe wird das Verhalten mit \( ε \) mit \( ε > 0\) untersucht:
1.)Ich suche nun den Funktionswert an der Stelle \(x=5+ε\):
\(f(5+ε)=\frac{2}{(5+ε)^2-5 \cdot (5+ε)}=\frac{2}{25+10ε+ε^2-25-5ε}= \frac{2}{ε^2+5ε}\)
Mit \( ε=\frac{1}{10}\) ist der Funktionswert:
\( \frac{2}{\frac{1}{100}+\frac{5}{10}}=\frac{200}{51}≈3,9\)
Mit \( ε=\frac{1}{100}\) ist der Funktionswert:
\( \frac{2}{\frac{1}{10000}+\frac{5}{100}}=\frac{20000}{501}≈39,9\)
Jetzt sieht man schon:
Wenn der Wert von \( ε \) sich immer mehr der 0 annähert, so steigt der Funktionswert immer weiter
Im Grenzfall mit ε=0 läuft der Funktionswert gegen \(+ ∞\)
2.)Ich suche nun den Funktionswert an der Stelle \(x=5-ε\):
\(f(5-ε)=\frac{2}{(5-ε)^2-5 \cdot (5-ε)}=\frac{2}{25-10ε+ε^2-25+5ε}= \frac{2}{ε^2-5ε}\)
Mit \( ε=\frac{1}{10}\) ist der Funktionswert:
\(\frac{2}{\frac{1}{100}-\frac{5}{10}}≈-4,1\)
Mit \( ε=\frac{1}{100}\) ist der Funktionswert:
\(\frac{2}{\frac{1}{10000}-\frac{5}{100}}≈-40,1\)
Auch hier sieht man:
Wenn der Wert von \( ε \) sich immer mehr der 0 annähert, so fällt der Funktionswert immer weiter
Im Grenzfall mit ε=0 läuft der Funktionswert gegen \(- ∞\)
Schaubild: