Umformen nach x (Lösung t=8)

Question

Aufgabe:

84=100-192*e^-25x/81      Die Gleichung soll nach x aufgelöst werden.

Problem/Ansatz: Da bei der Hochzahl durch 81 dividiert wird, komme ich beim Umformen nicht weiter. Es soll für t=8 ergeben.

Comments

Es soll für t=8 ergeben.

t kommt in der Aufgabe nicht vor.

Answer 1

192*e^(-25x/81) = 16

e^(-25x/81)= 16/192 = 1/12

-25x/81= ln(1/12)= ln1-ln12= -ln12

x= -ln(12)*81/25

Comments

Vielen Dank

---

Das Minuszeichen in der letzten Zeile ist falsch.

Answer 2

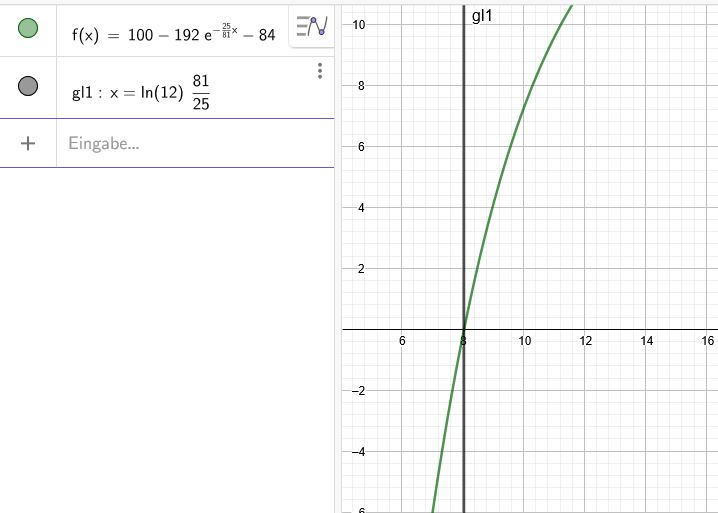
$84=100-192* e^{-\frac{25}{81}x} |-100$

$-16=-192* e^{-\frac{25}{81}x} | :(-16)$ 

$1=12* e^{-\frac{25}{81}x}$

$1=\frac{12}{ e^{\frac{25}{81}x} } |* e^{\frac{25}{81}x}$

$e^{\frac{25}{81}x}=12$

$e^{\frac{25}{81}x}=e^{ln(12)}$

Exponentenvergleich:

$\frac{25}{81}x=ln(12) |*\frac{81}{25}$

$x=ln(12)*\frac{81}{25}$

Comments

Super, Danke

---

Ab der vierten Zeile ist das Minuszeichen vor 25/81 verloren gegangen.

---

Ab der vierten Zeile ist das Minuszeichen vor 25/81 verloren gegangen.

$1=12* e^{-\frac{25}{81}x}$ ist identisch mit  $1=\frac{12}{ e^{\frac{25}{81}x} }$

---

Oh, da hast du recht. ggT hat den Vorzeichenfehler gemacht.