Wieso wird die 2 vor der Wurzel auf der linken Seite aufgelöst, wenn man diese mal 23 nimmt?

Question

Aufgabe:

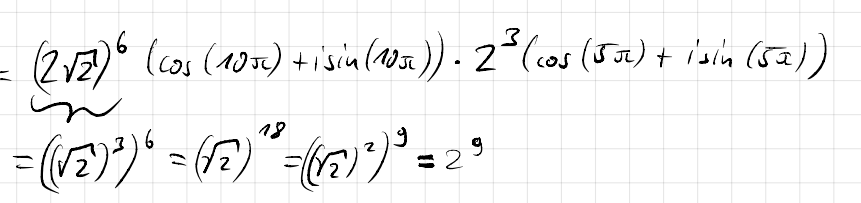
Text erkannt:

$\begin{array}{l}=\underbrace{(2 \sqrt{2})^{6}}(\cos (10 \pi)+i \sin (10 \pi)) \cdot 2^{3}(\cos (5 \pi)+i \sin (\sqrt{x})) \\ =\left((\sqrt{2})^{3}\right)^{6}=(\sqrt{2})^{18}=\left((\sqrt{2})^{2}\right)^{9}=2^{9}\end{array}$

Problem/Ansatz:

Ich verstehe nicht wieso aus 2*Wurzel 2⁶ * 2³ die 2 vor der Wurzel verschwindet in der Lösung darunter. Kann mir das mal jemand erläutern? Due restlichen Nachfolgenden Schritte mit den Potenzgesetzt etc verstehe ich

Answer 1

Offenbar wurde wegen $$2=\sqrt{2}\cdot\sqrt{2}$$ die $2$ mit der $\sqrt{2}$ zu $$\left(\sqrt{2}\right)^3$$ verschmolzen.

Comments

Danke! Ich habs verstanden!

Answer 2

Aloha :)

$$\phantom=\left(\pink2\sqrt2\right)^6=\left(\pink{\sqrt2\cdot\sqrt{2}}\cdot\sqrt2\right)^6=\left(\left(\sqrt2\right)^3\right)^6=\left(\sqrt{2}\right)^{3\cdot6}=\left(\sqrt2\right)^{18}=\left(\sqrt2\right)^{2\cdot9}$$$$=\left(\left(\sqrt2\right)^2\right)^9=2^9$$

Comments

Vielen dank für die Ausführliche Variante! Habs verstanden!!