Zeigen Sie, dass jede offene Kugel in R n einen C 1 -Rand hat

Question

Aufgabe:

Text erkannt:

Aufgabe 4 (5 Punkte)
(a) (1 Punkt) Zeigen Sie, dass jede offene Kugel in $\mathbb{R}^{n}$ einen $C^{1}$-Rand hat.
(b) (4 Punkte) Sei $D \subset \mathbb{R}^{n}$ eine Menge mit $C^{1}$-Rand und $U, h$ wie oben. Zeigen Sie, dass
$(\partial D) \cap U=\{x \in U: h(x)=0\}$.

Bräuchte hier Hilfe..
Das weiß ich, aber ich weiß nicht was ich damit mache

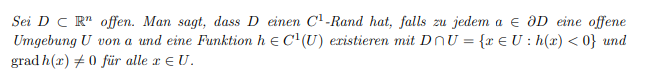
Text erkannt:

Sei $D \subset \mathbb{R}^{n}$ offen. Man sagt, dass $D$ einen $C^{1}$-Rand hat, falls zu jedem $a \in \partial D$ eine offene Umgebung $U$ von a und eine Funktion $h \in C^{1}(U)$ existieren mit $D \cap U=\{x \in U: h(x)<0\}$ und $\operatorname{grad} h(x) \neq 0$ für alle $x \in U$.

Comments

Wie wurde bei euch der Begriff der offenen Kugel eingeführt?

---

Ja wurde eingeführt.

Answer 1

(a) O.V.d.A. können wir uns auf den offenen Einheitsball $B\left( 0, 1\right) \subset \mathbf{R}^{n}$ beschränken. Sei nun $a \in \partial B( 0, 1)$
und $U = B\left( a, 1 / 2\right)$. Dann ist
$\begin{aligned} h\colon U \to \mathbf{R}, \quad h( x) = 1 - \left\| x\right\|_{2} \end{aligned}$
eine Funktion mit
$\begin{aligned} B\left( 0, 1\right) \cap U = \{ x \in U\mid h( x) < 0\} \end{aligned}$
und $\nabla f(x) \neq 0$ wie gefordert.

(b) Sei $a\in \partial D \cap U$ beliebig, es gilt also $h( a) \geqslant 0$. Dann existiert eine Folge $x_n \to a$ mit $x_{ n} \in D \cap U$ und somit folgt aufgrund der Stetigkeit von $h$
$\begin{aligned} \lim_{n \to\infty} h( x_{ n} ) = h( a) \geqslant 0 \implies h( a) = 0 \end{aligned}$
da $h( x_{ n} ) < 0$ für alle $x _{ n}$.

Für die andere Inklusion sei $x \in U$ mit $h( x) = 0$ und sei $B\left( x, \varepsilon\right)$ ein beliebig kleiner Ball um $x$ (der ganz in $U$ enthalten ist). Würde nun gelten, dass
$\begin{aligned} \forall y \in B\left( x, \varepsilon\right) \colon h( y) \geqslant 0 \end{aligned}$
so hätte $h$ in $x$ ein lokales Extremum woraus $\nabla f( x) = 0$ folgen würde, ein Widerspruch. Insbesondere existieren also $y _{ 1} , y_{ 2} \in B\left( x, \varepsilon\right)$
mit $h( y _{ 1} ) < 0$ also $y _{ 1} \in D$ und $h( y _{ 2} ) > 0$ also $y _{ 2} \in U \setminus ( D \cup \{ x\})$. Damit folgt $x \in \partial D$.

Comments

Danke,

aber eine Frage zur b):
Also wegen der stetigkeit ist lim h(x_n)=h(a) und der grenzwert ist ja größer gleich null aber dann muss h(a) = 0 ja nicht unbedingt sein oder?

Und muss ich am ende irgendwie noch begründen, dass x ∈ ∂D ? Wenn wir gezeigt haben, dass x nicht in D liegt, liegt es dann automatisch auf dem rand?

LG

---

Es muss $h(a) = 0$ gelten, denn würde $h(a) > 0$ sein, dann würde das ja der Stetigkeit von $h$ widersprechen, denn $h(x_n) <0$ für alle $x_n$. Oder anders gesagt: Der Grenzwert einer Folge deren Folgenglieder alle negativ sind, kann nicht positiv sein.

Zum zweiten Punkt: Ich habe ja genau gezeigt, dass $x \in \partial D$ gilt, vgl. die Definition des Randes einer Menge (Jede offene Umgebung enthält sowohl einen Punkt in $D$ als auch einen Punkt in $\mathbf{R}^n \setminus (D \cup \{x\})$

---

Ohh verstehe

Danke und LG