Zeigen sie: es existiert ein a ∈ A mit ||a-x0||2 = inf ||x-x0||2

Question

Aufgabe:

Sei \( A \subset \mathbb{R}^{n} \) abgeschlossen und konvex. Weiters sei \( x_{0} \in \mathbb{R}^{n} \backslash A \). Zeigen sie: es existiert ein \( a \in A \) mit
\( \left\|a-x_{0}\right\|_{2}=\inf _{x \in A}\left\|x-x_{0}\right\|_{2} . \)

Problem/Ansatz:

Zur Lösung kann man hier glaube ich die Vollständigkeit von \( \mathbb{R}^{n} \) sowie die Parallelogrammregel verwenden. Letztere würde ja, wenn ich richtig liege, für alle \( x, y, \in \mathbb{R}^{n} \) die folgende Darstellung liefern:
\( \|x+y\|_{2}^{2}+\|x-y\|_{2}^{2}=2\left(\|x\|_{2}^{2}+\|y\|_{2}^{2}\right) \)

Jetzt komm ich mit der Aufgabe aber trotzdem nicht weiter??

Answer 1

Hallo,

sei also \(x_0\in\mathbb{R}^n\setminus{A} \). Dann existiert eine Folge \((x_n)_{n\in\mathbb{N}}\subset A\) sodass

\( ||x_n - x_0||_2 \overset{(n\to\infty)}{\to} d \,:= \inf_{x\in A}||x-x_0||_2 \). Mit der von dir genannten Gleichung gilt weiter

\( ||x_n - x_m||^2 \)

\(= 2\cdot ||x_0-x_n||_2^2 + 2\cdot ||x_0-x_m||_2^2 - \underbrace{||2x_0 - x_n-x_m||^2_2}_{=4\cdot ||x_0-1/2\cdot(x_n+x_m)||_2^2 \geq 4\cdot d^2, \text{da }1/2\cdot(x_n+x_m)\in A}\)

\(\leq 2\cdot ||x_0-x_n||_2^2 + 2\cdot ||x_0-x_m||_2^2 - 4d^2 \overset{n,m\to\infty}{\longrightarrow}2d^2 + 2d^2 - 4d^2 = 0 \)

Damit ist \((x_n)\) Cauchy und da \(A\subseteq\mathbb{R}^n\) abgeschlossen ist, ist \(A\) vollständig und damit

existiert \(\lim_{n\to\infty}x_n = a\in A\), womit \(||x_0 - a||_2 = \lim_{n\to\infty}||x_0 - x_n|| = d\).

Comments

Man kann den Beweis übrigens völlig analog für beliebige Hilberträume \(H\) und \(\emptyset\neq A\subset H\) abgeschlossen und konvex führen.

Answer 2

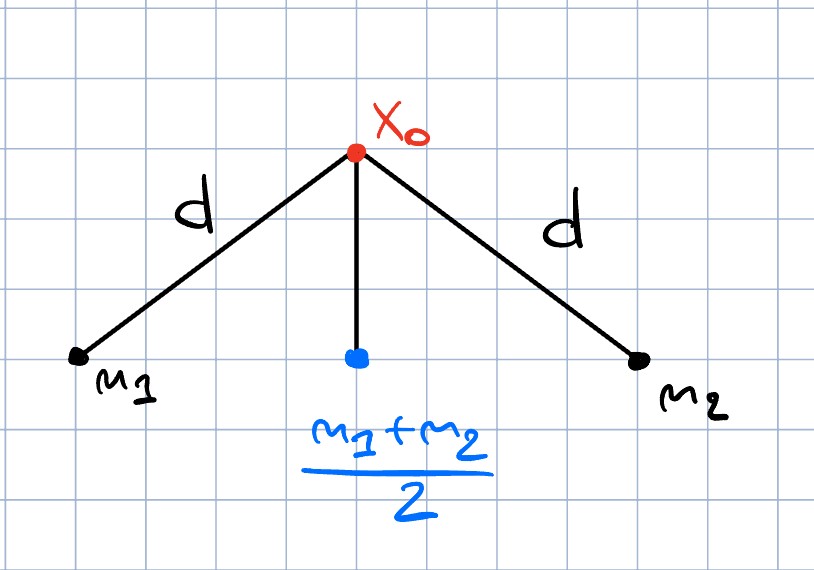
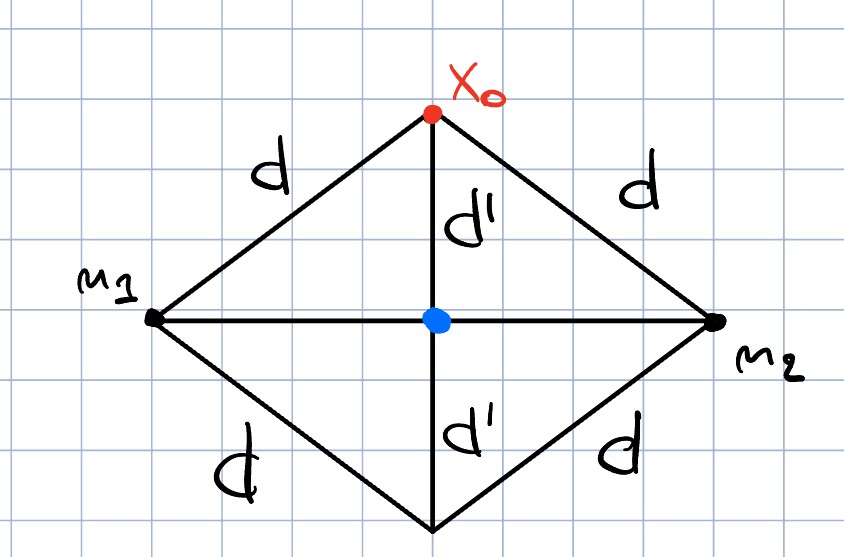
Die obige Antwort ist zwar richtig, ich möchte hier aber ein bisschen Intuition geben, weil die vielleicht hier ein bisschen zu kurz kommen kann: Wir haben
also irgendeine Folge \( \{ a_{ k} \}\subset A\) mit \( \left\| a_{ k}  - x_{ 0} \right\|_{ 2}  \to \inf_{ a\in A} \left\| a - x_{ 0} \right\|_{ 2}  \). Jetzt wollen
wir zeigen, dass \( a_{ k} \) konvergiert, und da \( A\) abgeschlossen ist, wird der Grenzwert auch in \( A\) liegen. Damit das überhaupt passieren kann,
muss jener Grenzwert \( a \in A\) (nehmen wir mal kurz die Existenz an) das einzige Element in \( A\) sein, welches eben diese Distanz zu \( x_{ 0} \) minimiert. Wäre
dies nämlich nicht der Fall, dann könnte ja die Folge \( a_{ k} \) immer zwischen den zwei Minimierern hin und her springen, also insbesondere nicht konvergieren.
Zuerst sollten wir also mal zeigen, dass wenn ein solcher Minimierer existiert, er der einzige ist.

Vergleiche dazu die beiden Bilder. Hier siehst du auch direkt, warum wir eigentlich die Parallelogramm Gleichung brauchen, denn mit dieser können wir zeigen, dass wenn es zwei solche Minimierer gäbe, wir einfach deren Mittelpunkt nemen könnten, und einen strikt besseren Minimierer hätten, was natürlich nicht geht (hier ist die Konvexität wichtig, welche garantiert, dass der Mittelpunkt auch wirklich drin liegt).

Comments

Danke für deine Ausführung - hilft wirklich sehr fürs allgemeine Verständnis der Thematik  ☺☺☺