Multivariante Optimierung von f(x,y) = -2x2 - y2 + 4x -3

Question

Die Aufgabe lautet: Die Funktion f, die für alle (x,y) durch f(x,y) = -2x²-y²+4x + 4y -3 definiert ist, hat ein Maximum. Bestimmen Sie die entsprechenden Werte von x und y.

Nun f₁'(x,y) und f₂'(x,y) konnte ich leicht berechnen. ich erhalte f₁'=-4x+4 und f₂'= -2y+4

Wie muss ich nun weiterfahren um die Punkte zu berechnen?

Comments

 f1' =- 4x+4  = 0
 x = 1
 f2' = -2y+4
  y = 2

 f1 '´ =- 4
 f2 ´´ = -2
 Die 2.Ableitung deutet auf ein Maximum hin.

  Ich würde die Ergebnisse so deuten, dass bei
x = 1 bei allen y ein Maximum ist.
Ebenso für y = 2 ist bei allen x ein Maximum.

  mfg Georg

Answer 1

Kurz gesagt, wenn es die Aufgabe aus dem Text sein soll:

$$f(x,y)=-2x^2-y^2+4x+4y-3=-2(x-1)^2-(y-2)^2+2+4-3$$

Woraus alles abzulesen ist.

Answer 2

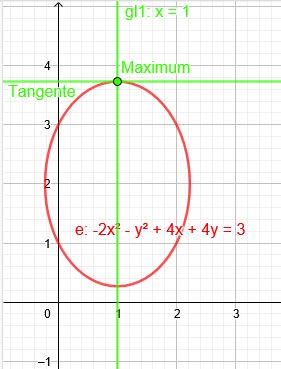
Die Aufgabe lautet: Die Funktion f, die für alle (x,y) durch $f(x,y) = -2x^2-y^2+4x + 4y -3$ definiert ist, hat ein Maximum. Bestimmen Sie die entsprechenden Werte von x und y.

$f(x,y) = -2x^2-y^2+4x + 4y -3$ 

Nach x abgeleitet:  $f_x(x,y) = -4x+4$

Nach y abgeleitet: $f_y(x,y) = -2y+4$

$f'(x)=-\frac{dx}{dy}=-\frac{-4x+4}{ -2y+4}$

Bei einem Extremwert ist die Tangentensteigung 0:

$-\frac{-4x+4}{ -2y+4}=0$

$-4x+4=0$

$x=1$    eingesetzt in  $-2x^2-y^2+4x + 4y =3$:

$-2-y^2+4 + 4y =3$

$y^2- 4y =-1$

$(y-2)^2=-1+4=3|±\sqrt{~~}$

1.)

$y-2=\sqrt{3}$

$y_1=2+\sqrt{3}$

2.)

$y-2=-\sqrt{3}$

$y_2=2-\sqrt{3}$

$y_1>y_2$

H$(1|2+\sqrt{3})$

Comments

Die Lösung ist falsch.

---

Wieso ist da kein Maximum?

---

Weil Dein Ansatz nicht funktioniert.

---

Weil es bei (1,0) ist.

---

Nein, bei (1,2)

---

Bei M$(1|2)$ ist der Mittelpunkt der Ellipse.

---

Ist Dir nicht aufgefallen, daß es hier um eine Funktion zweier Variabler geht?

---

ChatGPT:  Zusammenfassend hat die Funktion $f(x,y)$ ein Maximum bei $(x, y) = (1, 2)$ mit einem Funktionswert von $3$

Den Weg zu dieser Lösung verstehe ich aber nicht.

---

ACHTUNG: Überschrift und Aufgabentext stimmen nicht überein

---

ChatGPT hat recht.

Die Funktion sieht so aus:

Um Extremwerte zu berechnen kann man nicht wie bei einer Variablen vorgehen.

---

Wie sieht denn nun der Rechenweg zu dieser Lösung aus?

---

Ich hätte da eine Idee aber die paßt nicht auf den Rand der Seite :-)

Mathilf hat ja einen cleveren Weg angegeben, um das aus der Gleichung abzulesen. Im Allgemeinen ist das komplizierter.

Ernsthaft: google mal nach Funktionen mehrerer Variabler.

---

Das werde ich mal machen. Danke dir.

---

Bei y = 2 wird der Funktionswert kleiner als bei y = 0

---

Du hast wohl die Funktion aus der Überschrift und nicht aus dem Text genommen, stimmt dummerweise nicht überein.

---

Ja, hatte ich nicht gesehen. Auch nicht, dass die Frage 11 (in Worten: elf) Jahre alt ist.

Mein Kommentar betrifft die Funktion, wie sie im Titel steht.