Darstellung einer Potenzfunktion

Question

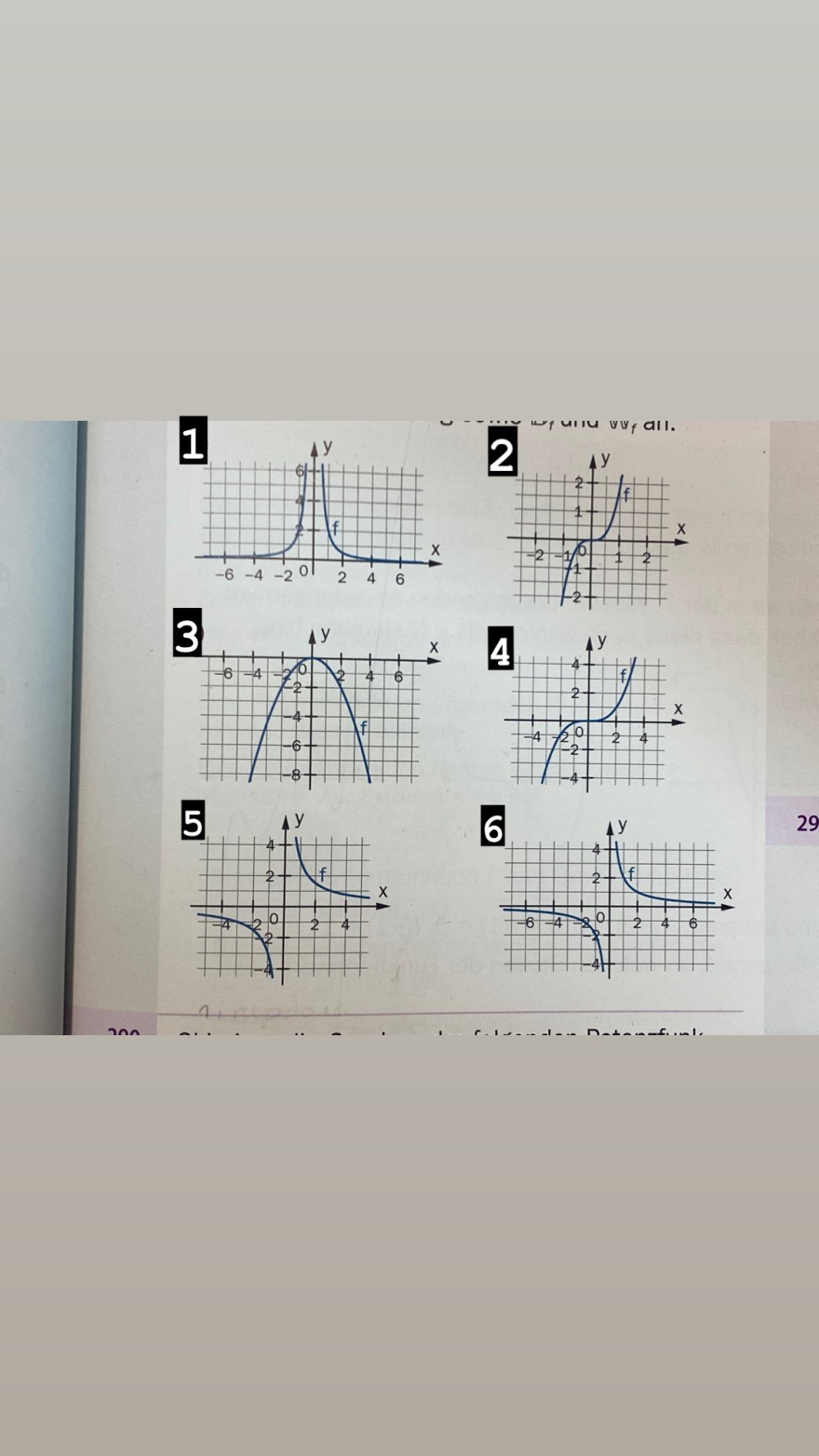
Aufgabe:

eine Potenzfunktion f mit f(x)=ax^z, a є R, z є {-2, -1, 0, 1, 2, 3} ist durch ihren Graphen gegeben. Gib die Termdarstellung sowie D_f und W_f an

Problem/Ansatz:

Text erkannt:

Eine Potenzfanktion of nit $f(x)=a \cdot x^{2}, \quad a \in R$,
$z \in\{-2 ;-1 ; 0 ; 1 ; 2 ; 3\}$ ist durch imren Graphen gegeben
Gil die Terndarstellung sowie Df und Wf an

Answer 1

1)

Plotlux öffnen

f₁(x) = 2/x²

2)

Plotlux öffnen

f₁(x) = 2x³

3)

Plotlux öffnen

f₁(x) = -1/2·x²

4)

Plotlux öffnen

f₁(x) = 1/8·x³

5)

Plotlux öffnen

f₁(x) = 3/x

6)

Plotlux öffnen

f₁(x) = 2/x

Answer 2

Sollst du die Darstellung der 6 Graphen  aufschreiben?

Dann ist wohl f(x)=ax^z, negative Exponenten haben die y Achse als Asymptoten ungerade Exponenten gehen bei x =0 gegen +∞ und -∞, gerade nur gegen +∞ oder nur gegen -∞ je nach Vorzeichen.

Positive Exponenten gerade symmetrisch zur y Achse, ungerade punktsymmetrisch zu (0|0).

Dann lies für a den Wert an einer ganzen Stelle  x ab z.B. für x=1.

Gruß lul