Aufgabe:
Hallo
hätte da eine Frage zur Teilaufgabe b und c. Muss man bei b auch das Oberflächenintegral der Deckel vom Zylinder berechnen? Und bei c meinte der Tutor man soll die Parametrisierung des Zylinders mit dem oberen und unteren Deckeln in die div F einsetzen.
Für Aufgabe und meine Teillösungen Siehe Bilder
Es würde mich echt freuen wenn jemand das beantworten kann .

Text erkannt:
3. Aufgabe: Satz von Gauß
Betrachten Sie das Vektorfeld \( F(x, y, z)=\left(4 x,-2 y^{2}, z^{2}\right) \) und den Zylinder
\( \mathcal{S}=\left\{(x, y, z) \in \mathbb{R}^{3}: x^{2}+y^{2}=4,0 \leq z \leq 3\right\} . \)
a) Bestimmen Sie eine Parametrisierung der Oberfläche \( \mathcal{S} \).
b) Berechnen Sie das Flussintegral \( I_{1}=\int \limits_{\mathcal{S}}\langle F, d \vec{O}\rangle \) mithilfe der gefundenen Parametrisierung.
c) Berechnen Sie jetzt das Flussintegral \( I_{1} \) mithilfe des Satzes von Gauß. Dafür brauchen Sie zuerst den Zylinder abzudecken.
Hinweis: Sie können das Integral \( \int \limits_{0}^{2 \pi} \cos ^{2} \theta d \theta=\pi \) benutzen.
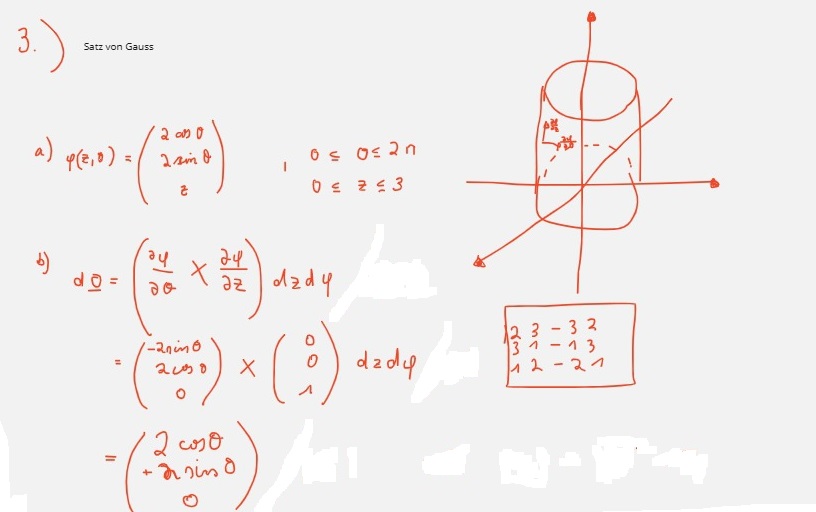
Text erkannt:
3. satzon Gauss
a) \( \varphi(z, \theta)=\left(\begin{array}{c}2 \cos \theta \\ 2 \sin \theta \\ z\end{array}\right), \begin{array}{l}0 \leq 0 \leq 2 n \\ 0 \leq z \leq 3\end{array} \)
b)
\( \begin{aligned} d \underline{\theta} & =\left(\frac{\partial \varphi}{\partial \theta} \times \frac{\partial \varphi}{\partial z}\right) d z d \varphi \\ & =\left(\begin{array}{c} -2 \sin \theta \\ 2 \cos \theta \\ 0 \end{array}\right) \times\left(\begin{array}{c} 0 \\ 0 \\ 1 \end{array}\right) d z d \varphi \\ & =\left(\begin{array}{c} 2 \cos \theta \\ +2 \sin \theta \\ 0 \end{array}\right) \end{aligned} \)
\( \begin{array}{lllll}2 & 3 & -3 & 2 \\ 3 & 1 & -1 & 3\end{array} \)

Text erkannt:
Nan dolot:
\( \begin{aligned} I_{1} & =\int \limits_{0}^{2 \pi} \int \limits_{0}^{3}\left(\begin{array}{c} 8 \cos \theta \\ -16 \sin ^{2} \theta \\ z^{2} \end{array}\right)\left(\begin{array}{c} 2 \cos \theta \\ +2 \sin \theta \\ 0 \end{array}\right) d z d \theta \\ & =\int \limits_{0}^{0} \int \limits_{0}^{3}\left(16 \cos ^{2} \theta-16 \sin ^{3} \theta\right) d z d \theta \end{aligned} \)
\( \longrightarrow \int \limits_{0}^{3} \int \limits_{0}^{2 \pi} 16 \cos ^{2} \theta d p d z-\int \limits_{0}^{3} \int \limits_{0}^{20} 16 \sin ^{3} 0 d y d z \)
mbequien rach
\( \stackrel{\varphi}{l} \quad 16 \pi \int \limits_{0}^{3} d z=16 \pi[z]_{0}^{3}=410 \)

Text erkannt:
c) \( \oiint_{R=\partial V} \underline{v} \frac{\underline{n}}{|\underline{n}|} d^{(h-1)} R=\int \limits_{V} d i v(\underline{u}) d^{l} V \)
\( \begin{array}{l} d \omega \underline{F}=4-4 y+2 z \\ g(r, \varphi, z)=\left(\begin{array}{c} r \cos \varphi \\ r \sin \varphi \\ z \end{array}\right) \end{array} \)
miro
LG