Extremalwertaufgabe - kürzester Abstand von einer Geraden und einem Graphen

Question

Hallo Miteinander,

Folgende Aufgabe: Welche Koordinaten hat der Punkt auf der Kurve f: y=e^x   , der von der Geraden g: y=3x-4 den kürzesten Abstand hat.
Meine Idee wäre nun die Steigung auf zwei verschiedene Arten anzugeben.

m= - 1/3(die 3 von der Geradensteigung)
 

m= y-y1/x-x1 , das Problem ist nun bei der Zweiten Steigungsformel, dass ich ja keinen konkreten Punkt habe, wo die Senkrechte nun startet.
Wie könnte ich dies doch lösen?

Viel Dank für eure Vorschläge.

Answer 1

Zunächst mal keine Antwort. Ich bekomme diese
Antwort aber nicht vollständig gelöscht.

mfg Georg

So 1 Tag später,

Grundsätzliche Überlegung :
ich verschiebe die Gerade zur Kurve hin. Der
Berührpunkt ist der Punkt mit dem geringsten
Abstand. Dies hatte ich mir selbst schon einmal
bewiesen und setze es hier voraus.

 

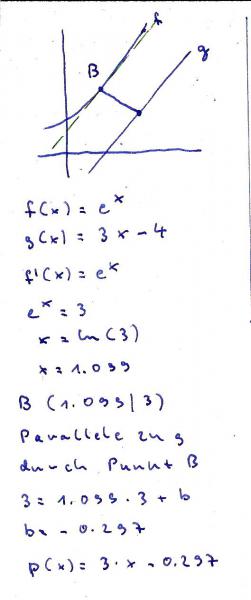
Die Steigung am Berührpunkt muß dieselbe Steigung
wie die Gerade haben, also 3.

Der Berührpunkt wird berechnet und die Gleichung
p ( x ) für die Parallele ermittelt.

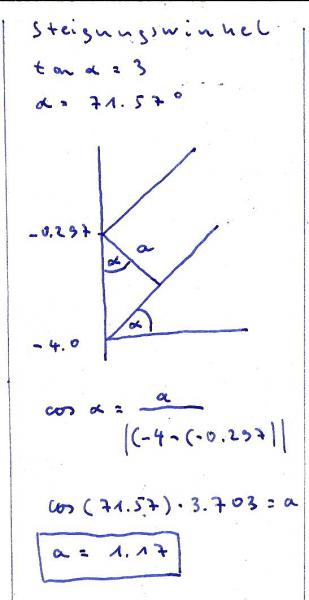
Über einen Vergleich der y-Achsenschnitte und des
Steigungswinkels erhalte ich das Ergebnis : kleinster
Abstand 1.17.

Bei Fehlern oder Fragen wieder melden.

mfg Georg