Aufgabe:
Hallo, benötige Hilfe beim berechnen eines "komplizierten" Integrals und zwar geht es um folgende Aufgabe d) die Berechnung von I2 (Siehe Bild).
Dabei gilt, dass v2 nicht konservativ.
Meine Teillösung siehe Bild
Problem/Ansatz:
Es geht um das unterstrichene DoppelIntegral amEnde
Text erkannt:
3. Aufgabe: Konservative Vektorfelde
Seien \( v_{1}, v_{2}: \mathbb{R}^{3} \rightarrow \mathbb{R}^{3} \) die Vektorfelde gegeben durch
\( v_{1}(x, y, z)=\left(2 x y+z^{3}, x^{2}, 3 x z^{2}\right), \quad v_{2}(x, y, z)=\left(e^{y}, x e^{y}, 2 z\right) \)
und \( \gamma_{1}:[0, \sqrt{\pi}] \rightarrow \mathbb{R}^{3}, \gamma_{2}:[0,1] \rightarrow \mathbb{R}^{3} \) die Kurven gegeben durch
\( \gamma_{1}(t)=\left(\cos t^{2}, \sin t^{2}, t^{2}\right), \quad \gamma_{2}(t)=\left(1+t \int \limits_{1}^{t} e^{u^{2}} d u, t, t^{2}\right) . \)
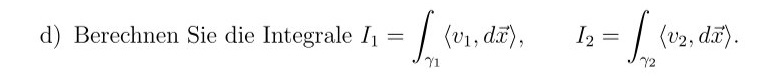
Text erkannt:
d) Berechnen Sie die Integrale \( I_{1}=\int \limits_{\gamma_{1}}\left\langle v_{1}, d \vec{x}\right\rangle, \quad I_{2}=\int \limits_{\gamma_{2}}\left\langle v_{2}, d \vec{x}\right\rangle \).

Text erkannt:
3.
a) notw. Bud :
\( \nabla \times v_{1}=\left(\begin{array}{c} 0-0 \\ 3 z^{2}-3 z^{2} \\ 2 x-2 x \end{array}\right)=0 \)
hims. Bed:
\( \nabla \cdot v_{1}=2 y+0+6 x z \neq 0 \)
\( \Rightarrow 0_{1} \) n. homenati
\( \begin{array}{l} \underline{v_{2}} \\ \nabla \times v_{2}=\left(\begin{array}{cc} 0 & -0 \\ 0-0 \\ e^{1}- & e^{y} \end{array}\right)=\delta \\ \nabla \cdot v_{2}=0+x e^{y}+2 \neq 0 \end{array} \)
\( v_{2} \) n. honsersatio
...
d) \( v_{2}\left(\gamma_{2}\right): \)
\( I_{2}=\int v_{2} d x=\int v_{2}\left(r_{2}(t) \cdot r_{2}^{\prime}(t) \cdot d t\right. \)
\( \begin{array}{l} \operatorname{mit} \gamma_{2}^{\prime}(t)=\left(\begin{array}{c} \int \limits_{1}^{t} e^{u^{2}} d u+t e^{t^{2}} \\ \hat{n}^{2 t} \end{array}\right), \frac{d}{d t} \int \limits_{a}^{t} f(x) d x=\frac{d}{d t}(F(t)-F(a))=f(t) \\ v_{2}\left(\gamma_{2}\right)=\left(e_{1}\left(\int \limits_{1}^{t} e^{u^{2}} d u+t e^{t^{2}}\right) e 1^{4 t}\right) \\ u_{2}\left(\gamma_{2}\right) \cdot \gamma_{2}^{2} t=e \cdot\left(\int \limits_{1}^{t} e^{u^{2}} d u+t e^{t^{2}}\right)+\left(\int \limits_{1}^{t} e^{u^{2}} d u+t e^{t^{2}}\right) e+8 t^{2} \\ \Rightarrow I_{2}=\int \limits_{0}^{1} 2 e\left(\int \limits_{1}^{t} e^{u^{2}} d u+t e^{t^{2}}\right)+8 t^{2} d t \\ =2 e(\int \limits_{0}^{1} t e^{t^{2}} d t+\underbrace{1}_{2} d t \int \limits_{1}^{t} d u e^{u^{2}})+\int \limits_{0}^{1} 8 t^{2} \\ \end{array} \)
miro