Vektorpotential gegeben durch f(x)

Question

Aufgabe:

Hallo, ist bei der Aufgabe (Siehe Bild 1) 1b) i die Lösung das f(x) jeden nur von x abhängige Funktion sein darf?

Text erkannt:

1. Aufgabe: Vektorpotentiale
a) Untersuchen Sie, ob die folgenden Vektorfelder \( \vec{v}_{1}, \vec{v}_{2}: \mathbb{R}^{3} \rightarrow \mathbb{R}^{3} \) ein Vektorpotential besitzen, und bestimmen Sie gegebenfalls ein Vektorpotential.
\( \vec{v}_{1}=\left(\begin{array}{c} \cos ^{2}(x) \\ y \cos (x)+y^{2} \\ -2 y z \end{array}\right), \quad \vec{v}_{2}=\left(\begin{array}{c} \sin (x)-x z \\ -y \cos (x) \\ \frac{1}{2} z^{2} \end{array}\right) \)
b) Sei \( f: \mathbb{R} \rightarrow \mathbb{R} \) eine \( \mathcal{C}^{1} \)-Funktion und \( \vec{v}_{3}: \mathbb{R}^{3} \rightarrow \mathbb{R}^{3} \) das Vektorfeld \( \vec{v}_{3}=(y z, x z, y f(x))^{T} \) :
(i) Untersuchen Sie, für welche Funktionen \( f \) das Vektorfeld \( \vec{v}_{3} \) ein Vektorpotential besitzt.
(ii) Falls \( f \) so eine Funktion ist, bestimmen Sie alle Vektorpotentiale \( \vec{u} \) der Form
\( \vec{u}=(L(x, y, z), M(y, z), 0)^{T}, \)
wobei \( L: \mathbb{R}^{3} \rightarrow \mathbb{R} \) und \( M: \mathbb{R}^{2} \rightarrow \mathbb{R} \mathcal{C}^{1} \)-Funktionen sind.

Es gilt ja (Siehe Bild 2)

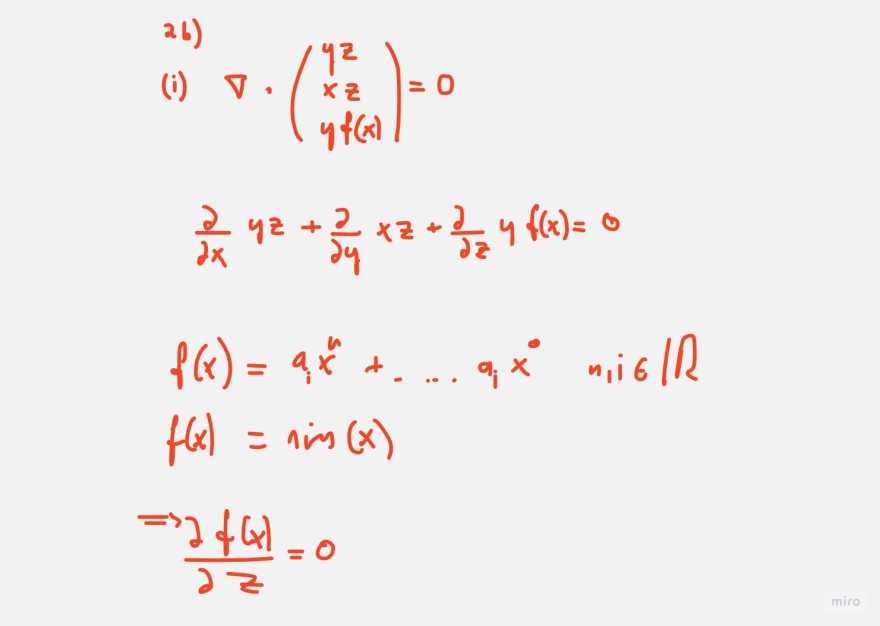
Text erkannt:

2b)
(i)
\( \begin{array}{l} \text { (i) } \nabla \cdot\left(\begin{array}{c} y z \\ x z \\ y f(x) \end{array}\right)=0 \\ \frac{\partial}{\partial x} y z+\frac{\partial}{\partial y} x z+\frac{\partial}{\partial z} y f(x)=0 \\ f(x)=a_{i} x^{u}+\ldots q_{i} x^{0} \quad n, i \in \mathbb{R} \\ f(x)=\operatorname{ing}(x) \\ \Rightarrow \frac{\partial f(x)}{\partial z}=0 \end{array} \)

Problem/Ansatz:

Da ja der 3 Term nur abhängt von y und f(x) bzw x

LG

Answer 1

Verstehe nicht, was Du da rechnest. Wieso sollte \(\nabla v_3=0\) sein?

Vielmehr ist eine Stammfunktion zu \(v_3\) gesucht, also ein Potenzial \(u\) mit \(\nabla u=v_3\).

Mach Dir die Begriffe klar, in allen Details.

Am einfachsten erledigt man (i) mit der notwendigen Bedingung (aus Deinen Vorlesungsunterlagen), dass, damit es ein Potenzial gibt, \({\rm rot\,} v_3=0\) (Nullvektor) sein muss.

Comments

Ja stimmt....Mach es dann jetzt

---

Text erkannt:

\( \begin{array}{l}\text { 1 b)(i) } \cot \underline{u}_{3}=0 \\ \left(\begin{array}{cl}f(x) & -x \\ y & -y f^{\prime}(x) \\ z & -z\end{array}\right)=0 \\ \text { I } f(x)=x \\ \text { II } f^{\prime}(x)=1 \\\end{array} \)

---

Ja, war auch mein Ergebnis.

Zur vollständigen Lösung gehört noch Text (Erklärungen, Begründungen).

---

Lösung ist leider falsch und bin jetzt wieder so schlau wie zu Anfang^^

Gesucht ist ja ein Vektorpotential, aber kein skalares.

---

Die Lösung für (i) ist richtig. Für (ii) hast Du noch nichts vorgelegt.

---

Der Tutor hat es folgendermaßen kommentiert:

rot v = 0 ist eine Notwendiige Bedingung dafür, dass v ein skalares Potential besitzt

Text erkannt:

1 b)(i) of \( \underline{v}_{3}=0 \quad \underline{v}_{3} \) soll Velctorpatentiol besitien
\( \begin{array}{l} \left(\begin{array}{cc} f(x) & -x \\ y & -y f^{\prime}(x) \\ z & -z \end{array}\right)=0 \\ I f(x)=x \\ \text { II } f^{\prime}(x)=1 \quad X \\ \end{array} \)

Habe es jetzt so

Text erkannt:

notw. Bed diof \( =0 \)
him. Red: \( \operatorname{rot} \underline{\omega}=\underline{v} \)
\( \Rightarrow \underbrace{\partial x y z}_{0}+\underbrace{\partial y x z}_{0}+\underbrace{\partial z y f(x)}_{0}=0 \)

---

Oha, ja, bitte vielmals um Entschuldigung, da hab ich nicht richtig gelesen. Ja, es geht um Vektorpotential, nicht Potential.

Und dann ist \(\text{div } \vec v_3=0\) eine notwendige Bedingung, genau wie Du von Anfang an gesagt hast, und das ist für alle \(f\) erfüllt. Sorry.

---

Ist überhaupt nicht schlimm.

Nur kann man dies als Lösung so angegeben, also dass es einfach für ALLE f gilt...? Oder sollte man noch sagen dass f stetig sein muss

---

Danke für die Nachsicht. Nach Vor. ist ja \(f\in C^1\), daher braucht man über weitere Voraussetzungen an \(f\) nicht nachzudenken.

---

Zu (ii): Ich komme auf

 \(L(x,y,z)=x\frac{z^2}2-f(x)\frac{y^2}2+l(x)\) und

 \(M(y,z)=-y\frac{z^2}2+m(y)\)

für beliebige \(l,m:\R\longrightarrow\R\).

---

cool,Danke.War gerad dabei. Die Konstante m(y) darf ja nicht von x abhängen. Das ist verständlich.

Das l(x) nicht von y abhängen darf, verstehe ich nicht. Es gilt ja L(x,y,z) also könnte man auch l(x,y) schreiben oder besser nicht?

---

Es muss ja \(\frac{\partial L}{\partial y}=-yf(x)\) sein, das geht nur, wenn \(l\) nicht von \(y\) abhängt.

---

Danke für den Tipp. So sollte jetzt eig stimmen.

Text erkannt:

(ii)
\( \begin{array}{l} \text { 1.) } y z=-\left\{z w_{y}=>w_{y}=-\int d z y z+C_{1}(x, y)=-\frac{1}{2} y z^{2}+C_{1}(x, y)\right. \\ \text { 2.) } x z=\partial_{z} v_{x} \Rightarrow w_{x}=\int d z x z+C_{2}(x, y)=\frac{x z^{2}}{2}+C_{2}(x, y) \\ \text { 3.) } y(x)=\partial x w_{1}-\partial y \omega_{x}=\partial_{x} C_{1}-\partial_{y} C_{2}(x, y) \\ y f^{\prime}(x)=\partial x C_{1}-\partial y C_{2}(x, y) \\ \end{array} \)

Sei \( C_{1}=m(y) \)
\( \begin{aligned} & -\int d y, y f(x)=C_{2}=-\frac{1}{2} f(x) y^{2}+A(x), \frac{\partial C_{2}}{\partial y}=-f(x) y \\ \Rightarrow & \vec{u}=(L(x, y, z), M(y, z), 0)^{\top}=\left(\begin{array}{c} \frac{x z^{2}}{2}-\frac{1}{2} f(x) g^{2}+A(x) \\ -\frac{1}{2} y z^{2}+m(y) \\ 0 \end{array}\right) \end{aligned} \)

Prole:
\( \operatorname{vov} \vec{u}=\left(\begin{array}{c} 0--y z \\ x z \\ f(x) y \end{array}\right) \)
miro

---

Ich finde das etwas unübersichtlich, ich selbst verwende andere Schreibweisen. Aber wenn am Ende das (aus meiner Sicht) richtige rauskommt, ist es ja gut.

Prüfe aber noch, ob Du das nicht straffen kannst, denn nach Vorgabe ist ja \(\partial x w_y=0\).

Eine Probe ist immer sinnvoll, allerdings zeigt die hier nicht, dass man alle Möglichkeiten gefunden hat - ohne A(x) und m(y) würde die Probe ja auch klappen.

Dass man alle Möglichkeiten gefunden hat, sieht man an der Herleitung.