Rotationsvolumen von f(x)=x-2*x2

Question

Aufgabe:

Ich möchte für die Funktion f(x)=x-2*x² das Rotationsvolumen im xe[0;3] berechnen. Ich habe da 612*pi/5 raus, bin mir aber nicht sicher, weil man ja eigentlich die Umkehrfunktion bilden müsste, weil die Funktion um die Ordinate rotiert, oder nicht?

Ich würde mich über eine Erklärung freuen :)

Comments

weil man ja eigentlich die Umkehrfunktion bilden müsste, weil die Funktion um die Ordinate rotiert

Wenn die Aufgabe das vorgibt, dann ja. Wenn nicht, dann nicht. Standardmäßig meint man aber die Rotation um die Abszisse.

---

Um welche Achse soll denn rotiert werden?

---

Um welche Achse soll denn rotiert werden?

weil man ja eigentlich die Umkehrfunktion bilden müsste, weil die Funktion um die Ordinate rotiert,

Damit ist die Achse doch genannt, oder?

---

Ach ok, das habe ich übersehen....

Answer 1

Aloha :)

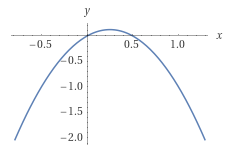
Bei der Rotation des Graphen der Funktion$$y(x)=x-2x^2=-2\left(x^2-\frac12x\pink{+\frac{1}{16}}\right)\pink{+\frac18}=\frac18-2\left(x-\frac14\right)^2$$im Intervall $x\in[0;3]$ um die y-Achse, musst du den Hochpukt $H\left(\frac14|\frac18\right)$ beachten. Für $x<\frac14$ fällt die Funktion nämlich wieder ab, sodass im Rotationsvolumen eine kleine Wölbung entsteht, die subtrahiert werden muss.

Das heißt formal:$$V=\int\limits_{y(3)}^{y(\frac14)}\pi\,x^2\,dy-\int\limits_0^{y(\frac14)}\pi\,x^2\,dy$$Beachte, dass die Integrationsgrenzen so gewählt sind, dass wir in Richtung der y-Achse von unten nach oben integrieren. Wir berechnen die Integrale mit Substitution:$$V=\int\limits_{x=3}^{\frac14}\pi\,x^2\,\frac{dy}{dx}\,dx-\int\limits_{x=0}^{\frac14}\pi\,x^2\,\frac{dy}{dx}\,dx=\int\limits_{x=3}^{\frac14}\pi\,x^2(1-4x)\,dx-\int\limits_{x=0}^{\frac14}\pi\,x^2(1-4x)\,dx$$$$\phantom V=\pi\left[\frac{x^3}{3}-x^4\right]_{x=3}^{\frac14}-\pi\left[\frac{x^3}{3}-x^4\right]_{x=0}^{\frac14}=\pi\left(\frac{1}{768}-(-72)\right)-\pi\left(\frac{1}{768}-0\right)$$$$\phantom V=72\,\pi$$

Comments

Danke dir :) Sehr ausführlich

Answer 2

Ja.

https://www.frustfrei-lernen.de/mathematik/rotationsvolumen-volumen-…

y= x-2x² = -2x²+x = -2(x²-0,5x+0,25²-0,25²) = -2(x-0,25)² + 0,0625

(y-0,0625)/-2 = (x-0,25)²

x=  ((y-0,0625)/-2))^(1/2) +0,25

Dann x und y vertauschen:

y^-1 = ...

Comments

Eine Skizze kann außerdem hilfreich sein.