Berechnung des Kurvenintegrals mit dem Tangentialvektor. Umformung unklar.

Question

Moin,

Ich habe eine Frage zu folgender Umformung.

Ich komme dort leider nicht weiter, hat da einer vielleicht eine Idee?

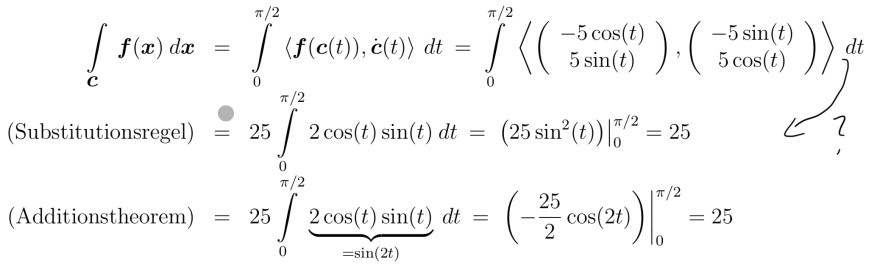
Text erkannt:

$\begin{aligned} \int \limits_{\boldsymbol{c}} \boldsymbol{f}(\boldsymbol{x}) d \boldsymbol{x} & =\int \limits_{0}^{\pi / 2}\langle\boldsymbol{f}(\boldsymbol{c}(t)), \dot{\boldsymbol{c}}(t)\rangle d t=\int \limits_{0}^{\pi / 2}\left\langle\left(\begin{array}{c}-5 \cos (t) \\ 5 \sin (t)\end{array}\right),\left(\begin{array}{c}-5 \sin (t) \\ 5 \cos (t)\end{array}\right)\right\rangle d t \\ \text { (Substitutionsregel) } & =25 \int \limits_{0}^{\pi / 2} 2 \cos (t) \sin (t) d t=\left.\left(25 \sin ^{2}(t)\right)\right|_{0} ^{\pi / 2}=25 \\ \text { (Additionstheorem) } & =25 \int \limits_{0}^{\pi / 2} \underbrace{2 \cos (t) \sin (t)}_{=\sin (2 t)} d t=\left.\left(-\frac{25}{2} \cos (2 t)\right)\right|_{0} ^{\pi / 2}=25\end{aligned}$

Answer 1

Im Integral steht das Skalarprodukt. Multipliziere die jeweils die ersten Komponenten und zweiten Komponenten und addiere diese Produkte.