Question

Sarah und Kim tragen ein Tennismatch mit drei Runden aus.

Sarah gewinnt hierbei mit einer Wahrscheinlichkeit von 60%; Kim mit 40%.

Das gesamte Tennismatch gewinnt diejenige, die mindestens zwei Runden gewonnen hat.

a) Mit welcher Wahrscheinlichkeit gewinnt Kim, obwohl Sarah das erste Spiel gewonnen hat (bitte mit Baumdiagramm).

b) Mit welcher Wahrscheinlichkeit gewinnt Kim das gesamte Match? Zähle die anderen Möglichkeiten hinzu ( auch mit Baumdiagramm).

c) Wenn Kim ein Spiel gewinnt, motiviert sie das so,dass beide Mädchen gleich gut spielen.

Verliert sie allerdings,verlässt sie auch der Mut wieder und es gelten die alten Wahrscheinlichkeiten.

Wie sehen die Ergebnisse dann aus?


könnt ihr mir helfen bitte

Answer 1

 

zu a) und b) passt das folgende Baumdiagramm:

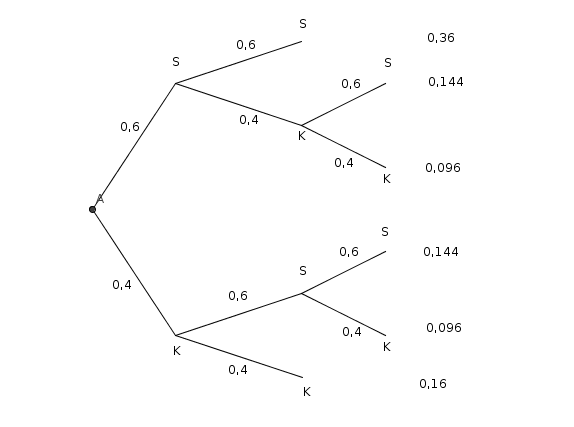
a) Mit welcher Wahrscheinlichkeit gewinnt Kim, obwohl Sarah das erste Spiel gewonnen hat (bitte mit Baumdiagramm)?

0,096/(0,36 + 0,144 + 0,096) = 0,16 = 16%

 

b) Mit welcher Wahrscheinlichkeit gewinnt Kim das gesamte Match? Zähle die anderen Möglichkeiten hinzu (auch mit Baumdiagramm).

Kim gewinnt das gesamte Match mit einer Wahrscheinlichkeit von 0,096 + 0,096 + 0,16 = 0,352 = 35,2%

 

c) Wenn Kim ein Spiel gewinnt, motiviert sie das so,dass beide Mädchen gleich gut spielen. Verliert sie allerdings, verlässt sie auch der Mut wieder und es gelten die alten Wahrscheinlichkeiten.
Wie sehen die Ergebnisse dann aus?

Dann ergibt sich folgendes Baumdiagramm (die Veränderungen habe ich mit * kenntlich gemacht):

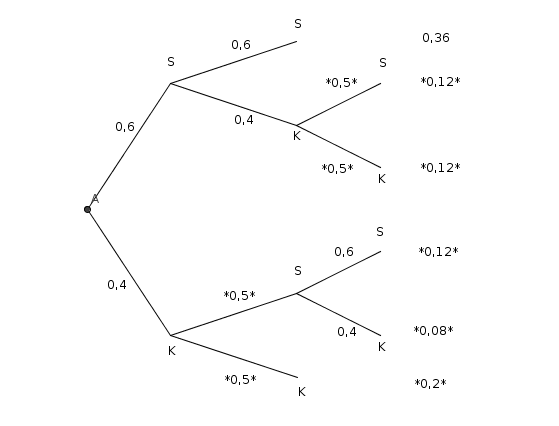
Wahrscheinlichkeit, dass Kim gewinnt, obwohl Sarah das 1. Spiel gewonnen hat: 0,4 * 0,5 = 0,2 = 20%

oder wie oben gerechnet: 0,12/(0,36 + 0,12 + 0,12) = 0,12/0,6 = 0,2 = 20%

 

W., dass Kim das gesamte Match gewinnt: 0,12 + 0,08 + 0,2 = 0,4 = 40%

 

Besten Gruß