Aufgabe:
Stimmt meine Ortskurve?
Text erkannt:
fa(x)=xa⋅eax=1ax⋅eaxfa′(x)=eax⋅(1a+x)T(−1a(0,37⋅(−1a2))y=0,37⋅(−1a2)x=−1ay=0,37⋅(−1−1a)2)y=0,37⋅(−11a2)=0,37⋅(−a2)=−0,37a2 \begin{array}{l}f_{a}(x)=\frac{x}{a} \cdot e^{a x}=\frac{1}{a} x \cdot e^{a x} \\ f_{a}^{\prime}(x)=e^{a x} \cdot\left(\frac{1}{a}+x\right) \quad T\left(-\frac{1}{a}\left(0,37 \cdot\left(-\frac{1}{a^{2}}\right)\right)\right. \\ y=0,37 \cdot\left(-\frac{1}{a^{2}}\right) \quad x=-\frac{1}{a} \\ y=0,37 \cdot\left(-\frac{1}{\left.-\frac{1}{a}\right)^{2}}\right) \\ y=0,37 \cdot\left(-\frac{1}{\frac{1}{a^{2}}}\right)=0,37 \cdot\left(-a^{2}\right)=-0,37 a^{2}\end{array} fa(x)=ax⋅eax=a1x⋅eaxfa′(x)=eax⋅(a1+x)T(−a1(0,37⋅(−a21))y=0,37⋅(−a21)x=−a1y=0,37⋅(−−a1)21)y=0,37⋅(−a211)=0,37⋅(−a2)=−0,37a2
Problem/Ansatz:
Du hast am Ende x durch einen Term mit a ersetzt. Du musst es aber genau umgekehrt machen. Und warum ersetzt du einen klaren genauen Wert 1/e durch diesen unsäglichen Näherungswert 0,37?
https://www.schullv.de/mathe/basiswissen/analysis/kurvendiskussion/o…
Ähm mir war so, dass man den x- Wert durch den y-Wert ersetzt. Wie würde man denn genau korrekterweise vorgehen
Du hast nicht geschrieben, dass es um die Ortskurve der Extrema geht. Deine Ableitung ist richtig. Diese ist Null für a=-1x \frac{1}{x} x1. Wenn man a in der Funktionenschar durch -1x \frac{1}{x} x1 ersetzt, erhält man nach etwas Umformung g(x)= - x2e \frac{x^2}{e} ex2 als Funktionsgleichung der Ortskurve der Extrema.
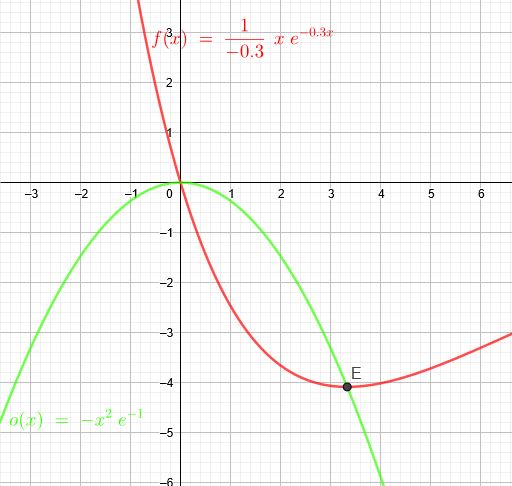
fa(x)=1a⋅x⋅ea⋅xf_a(x)= \frac{1}{a}\cdot x \cdot e^{a \cdot x}fa(x)=a1⋅x⋅ea⋅x
fa′(x)=1a⋅ea⋅x+1a⋅x⋅ea⋅x⋅a=1a⋅ea⋅x+x⋅ea⋅xf'_a(x)= \frac{1}{a} \cdot e^{a \cdot x}+\frac{1}{a}\cdot x \cdot e^{a \cdot x}\cdot a= \frac{1}{a} \cdot e^{a \cdot x}+ x \cdot e^{a \cdot x}fa′(x)=a1⋅ea⋅x+a1⋅x⋅ea⋅x⋅a=a1⋅ea⋅x+x⋅ea⋅x
1a⋅ea⋅x+x⋅ea⋅x=0 \frac{1}{a} \cdot e^{a \cdot x}+ x \cdot e^{a \cdot x}=0a1⋅ea⋅x+x⋅ea⋅x=0 ea⋅x≠0e^{a \cdot x}≠0ea⋅x=0
x=−1a x=-\frac{1}{a}x=−a1 fa(−1a)=1a⋅(−1a)⋅ea⋅(−1a)=−1a2⋅e−1f_a(-\frac{1}{a})= \frac{1}{a}\cdot (-\frac{1}{a})\cdot e^{a \cdot (-\frac{1}{a})}=-\frac{1}{a^2} \cdot e^{-1}fa(−a1)=a1⋅(−a1)⋅ea⋅(−a1)=−a21⋅e−1
x=−1a x=-\frac{1}{a}x=−a1 nach a auflösen : a=−1x a=-\frac{1}{x}a=−x1 und in fa(−1a)=−1a2⋅e−1f_a(-\frac{1}{a})=-\frac{1}{a^2} \cdot e^{-1}fa(−a1)=−a21⋅e−1 einsetzen:
Ortskurve:
o(x)=−1(−1x)2⋅e−1=−x2⋅e−1o(x)=-\frac{1}{(-\frac{1}{x})^2} \cdot e^{-1}=-x^2 \cdot e^{-1}o(x)=−(−x1)21⋅e−1=−x2⋅e−1
Für die Ortskurve möchtest du am Ende einen Ausdruck y=… y= \ldots y=…, der (meistens) von x x x abhängt. Bei der Berechnung von Extrem- oder Wendepunkten bekommst du in der Regel bei beiden Koordinaten eine Abhängigkeit des Parameters, sagen wir zum Beispiel H(2a∣a2) H(2a | a^2) H(2a∣a2). Diese Koordinaten können wir als Gleichung aufschreiben, denn es gilt x=2a x=2a x=2a und y=a2 y=a^2 y=a2. Wenn wir uns nun y y y anschauen, sehen wir, dass die Abhängigkeit von x x x fehlt, weil es dort nicht vorkommt. Wir können aber mithilfe der xx x-Koordinate das a a a durch x x x darstellen. Einfaches umstellen liefert nämlich a=x2 a = \frac{x}{2} a=2x. Das können wir nun anstelle von a a a einsetzen. Damit erhält man in diesem Fall die Ortskurve y=(x2)2 y=\left( \frac{x}{2} \right)^2 y=(2x)2.
Dieses Vorgehen funktioniert immer. Tipp: Manchmal muss man nicht nach a a a auflösen. Betrachte zum Beispiel H(a2∣a2) H(a^2 | a^2) H(a2∣a2). Dann gilt y=a2 y=a^2 y=a2 und x=a2 x=a^2 x=a2. Dann kann man das a2 a^2 a2 aber direkt durch x x x ersetzen und man erhält die Ortskurve y=x y=x y=x.
Ein anderes Problem?
Willkommen bei der Mathelounge! Stell deine Frage einfach und kostenlos
