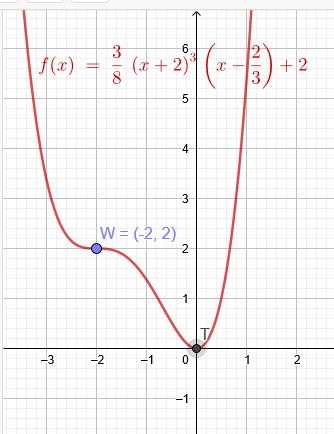
… Der Graph der ganzrationalen Funktion h vierten Grades hat in \(O (0|0)\) und im Wendepunkt \(W (-2|\red{2})\) Tangenten parallel zur x- Achse.
Da der Weg per Gauß schon dargelegt wurde, hier eine andere Möglichkeit:
Ein Wendepunkt \(W (-2|2)\) Tangente parallel zur x- Achse bedeutet, dass hier ein Sattelpunkt vorliegt:
Deshalb verschiebe ich den Graph um \(\red{2}\) Einheiten nach unten: \(W´ (-2|0)\) Hier ist nun eine dreifache Nullstelle:
\(f(x)=a(x+2)^3(x-N)\)
\(O (0|0)\)→ \(O´ (0|-2)\):
\(f(0)=a(0+2)^3(0-N)=-8aN=-2\)→ \(a=\frac{1}{4N}\)
\(f(x)=\frac{1}{4N}(x+2)^3(x-N)\)
parallele Tangente bei \(O´ (0|...)\):
\(f'(x)=\frac{1}{4N}[3(x+2)^2(x-N)+(x+2)^3]\)
\(f'(0)=\frac{1}{4N}[3\cdot(0+2)^2(0-N)+(0+2)^3]=0\) \(N=\frac{2}{3}\) \(a=\frac{1}{4\cdot \frac{2}{3}}=\frac{3}{8}\)
\(f(x)=\frac{3}{8}(x+2)^3(x-\frac{2}{3})\)
\(\red{2}\) Einheiten nach oben:
\(h(x)=\frac{3}{8}(x+2)^3(x-\frac{2}{3})+2\)