Lineare Algebra und Matrix M

Question

Aufgabe:

Text erkannt:

Eine der Geraden ist die Wendetangente der Kostenfunktion $\mathrm{K}$ aus (1.1.1), eine andere der Geraden ist die Tangente von $K$ an der Stelle $\mathrm{X}_{\mathrm{BM}}$ (Betriebsminimum).
1.2.1 Entscheiden Sie für die beiden Tangenten auf Grundlage geeigneter Berechnungen, welche der angegebenen Geradengleichungen dazugehört.
7
1.3 Lineare Algebra

Gegeben ist die Matrix $M=\left(\begin{array}{cc}1 & 3 \\ 1 & -1\end{array}\right)$.
1.3.1 Für jeden Vektor $\vec{u}=\left(\begin{array}{l}u_{1} \\ u_{2}\end{array}\right)$ mit $u_{1}, u_{2} \in \mathbb{R}$ gilt $M^{2} \cdot \vec{u}=a \cdot \vec{u}$, wobei a eine reelle Zahl ist. Ermitteln Sie den Wert von a.
2
1.3.2 Bestimmen Sie alle Vektoren $\vec{v}=\left(\begin{array}{l}v_{1} \\ v_{2}\end{array}\right)$ mit $v_{1}, v_{2} \in \mathbb{R}$, für die $M \cdot \vec{v}=2 \cdot \vec{v}$ gilt.
3

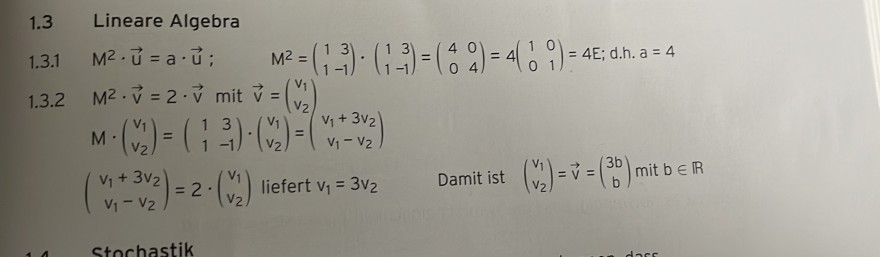
Text erkannt:

1.3 Lineare Algebra
1.3.1 $\quad M^{2} \cdot \vec{u}=a \cdot \vec{u} ; \quad M^{2}=\left(\begin{array}{rr}1 & 3 \\ 1 & -1\end{array}\right) \cdot\left(\begin{array}{rr}1 & 3 \\ 1 & -1\end{array}\right)=\left(\begin{array}{ll}4 & 0 \\ 0 & 4\end{array}\right)=4\left(\begin{array}{ll}1 & 0 \\ 0 & 1\end{array}\right)=4 E ; d \cdot h \cdot a=4$
1.3.2 $M^{2} \cdot \vec{v}=2 \cdot \vec{v}$ mit $\vec{v}=\left(\begin{array}{l}v_{1} \\ v_{2}\end{array}\right)$
$M \cdot\left(\begin{array}{l} v_{1} \\ v_{2} \end{array}\right)=\left(\begin{array}{cc} 1 & 3 \\ 1 & -1 \end{array}\right) \cdot\left(\begin{array}{l} v_{1} \\ v_{2} \end{array}\right)=\left(\begin{array}{l} v_{1}+3 v_{2} \\ v_{1}-v_{2} \end{array}\right)$
$\left(\begin{array}{c}v_{1}+3 v_{2} \\ v_{1}-v_{2}\end{array}\right)=2 \cdot\left(\begin{array}{l}v_{1} \\ v_{2}\end{array}\right)$ liefert $v_{1}=3 v_{2} \quad$ Damit ist $\left(\begin{array}{l}v_{1} \\ v_{2}\end{array}\right)=\vec{v}=\left(\begin{array}{c}3 b \\ b\end{array}\right)$ mit $b \in \mathbb{R}$

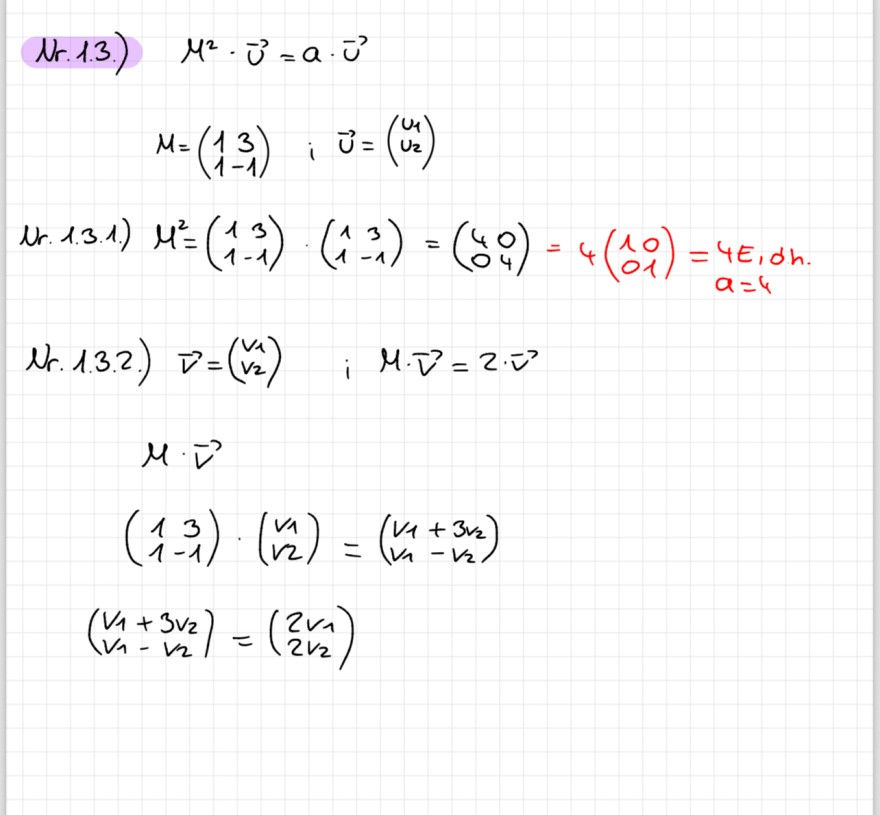
Text erkannt:

Nr.1.3.)
$\begin{array}{c} M^{2} \cdot \vec{u}=a \cdot \vec{u} \\ M=\left(\begin{array}{cc} 1 & 3 \\ 1 & -1 \end{array}\right) \quad ; \quad \vec{u}=\left(\begin{array}{l} u_{1} \\ v_{2} \end{array}\right) \end{array}$

Ur. 1.3.1.) $M^{2}=\left(\begin{array}{cc}1 & 3 \\ 1 & -1\end{array}\right) \cdot\left(\begin{array}{cc}1 & 3 \\ 1 & -1\end{array}\right)=\left(\begin{array}{ll}4 & 0 \\ 0 & 4\end{array}\right)=4\left(\begin{array}{ll}1 & 0 \\ 0 & 1\end{array}\right)=4 E_{1} d h$. $a=4$

Nr. 1.3.2.) $\vec{v}=\left(\begin{array}{l}v_{1} \\ v_{2}\end{array}\right) \quad ; \quad M \cdot \vec{v}=2 \cdot \vec{v}$
$\begin{array}{c} \mu \cdot \vec{v} \\ \left(\begin{array}{cc} 1 & 3 \\ 1 & -1 \end{array}\right) \cdot\left(\begin{array}{l} v_{1} \\ v_{2} \end{array}\right)=\left(\begin{array}{l} v_{1}+3 v_{2} \\ v_{1}-v_{2} \end{array}\right) \\ \left(\begin{array}{l} v_{1}+3 v_{2} \\ v_{1}-v_{2} \end{array}\right)=\left(\begin{array}{l} 2 v_{1} \\ 2 v_{2} \end{array}\right) \end{array}$

Ich verstehe bei Aufgabe 1.3.2 nicht, wie die auf 3v2 gekommen sind. Ich habe auch meinen Ansatz hochgeladen.

Answer 1

Stelle zum Beispiel die letzte Ziele in deiner Rechnung nach $v_1$ um.

Comments

Text erkannt:

oHimi 2019 neu
$\begin{array}{l} \left(\begin{array}{cc} 1 & 3 \\ 1 & -1 \end{array}\right) \cdot\left(\begin{array}{l} v_{1} \\ v_{2} \end{array}\right)=\left(\begin{array}{l} v_{1}+3 v_{2} \\ v_{1}-v_{2} \end{array}\right) \\ \left(\begin{array}{l} v_{1}+3 v_{2} \\ v_{1}-v_{2} \end{array}\right)=\left(\begin{array}{l} 2 v_{1} \\ 2 v_{2} \end{array}\right) \\ I \cdot v_{1}+3 v_{2}=2 v_{1} \mid+v_{1} \\ 3 v_{2}=3 v_{1} 1: 3 \\ =v_{1} \end{array}$

da bleibt keine Zahl übrig

---

Du musst $-v_1$ rechnen. ;)

---

Ja hab’s gesehen Danke

und woher weiß ich was v2 dann ist?

---

Dann ist $v_2=\frac{1}{3}v_1$.

---

wieso 1/3 dachte wäre 1?

---

Weil $v_1=3v_2$. Daraus folgt $v_2=\ldots$? Es gibt hier keine feste Zahl, weil es unendlich viele solcher Vektoren gibt.