binomialverteilung Wahrscheinlichkeit bestimmen

Question

Hallo, man soll diese Aufgabe ohne Taschenrechner lösen.

Die Zufallsgröße $X$ ist binomialverteilt mit den Parametern $n=100$ und $p$. Der Erwartungswert von $\mathrm{X}$ ist 50 .

a) Die Wahrscheinlichkeit $P(X \geq 61)$ beträgt etwa $2 \%$. Bestimmen Sie unter Verwendung dieses Werts den zugehörigen Wert für die Wahrscheinlichkeit $\mathrm{P}(40 \leq \mathrm{X} \leq 60)$.

Answer 1

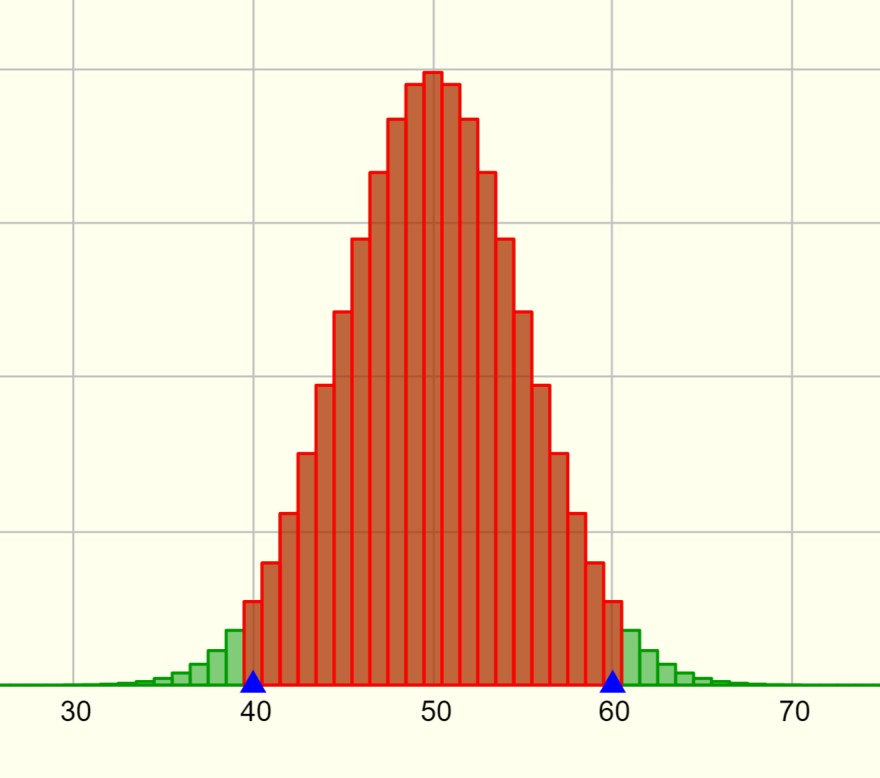
Man sollte erkennen, dass das Intervall $[40;60]$ ein um den Erwartungswert symmetrisches Intervall ist. Wegen $p=0,5$ ($100 \cdot p = 50$) ist die Verteilung symmetrisch, so dass man mit Hilfe von $P(X\geq 61)$, was außerhalb dieses Intervalls liegt, darauf schließen kann, wie groß dann die Wahrscheinlichkeit sein muss, dass $X$ innerhalb des Intervalls liegt.

Es hilft bei solchen Aufgaben, sich das ganze in Form einer Wahrscheinlichkeitsverteilung zu veranschaulichen.

Answer 2

$n=100$ und $p$. Der Erwartungswert von $\mathrm{X}$ ist 50 .

Also ist p=0,5.

Damit ist die Wahrscheinlichkeitsverteilung symmetrisch, und

 $P(X \geq 61)$= $P(X \leq 49)$.

Kannst du damit  $\mathrm{P}(40 \leq \mathrm{X} \leq 60)$ berechnen?

Comments

Kann es sein, dass die $49$ eine $39$ sein sollte?

---

Ich weiß grade nicht weiter. Wie weiß ich dass  $P(X \geq 61)$= $P(X \leq 49)$ gilt?

---

61+49 = 110

-----------------------

---

Ja, es muss natürlich $P(X \geq 61)$= $P(X \leq 39)$ heißen.

Answer 3

P(40<=X<=60) = P(X<=60)- P(X<=39)

P(X<=60) = 0,98

P(X<=39) = 0,02

P(40<=X<=60)= 0,98-0,02 = 0,96

Comments

Okay verstehe, wie bist du aber auf die 0,02 gekommen?