Ellipse in Viereck einschreiben

Question

Aufgabe:

Ein Viereck hat die Ecken mit den Koordinaten A(0│0), B(3│0), C(4│4) und D(0│2). Beschreiben Sie eine Ellipse in das Viereck ein, welche alle vier Seitenlinien berührt, mit

a) maximalem Flächeninhalt

b) minimaler Exzentrizität.

Problem/Ansatz:

Bin gestern auf diese Aufgabe gestoßen. Vielleicht möchte sich gelegentlich noch jemand damit beschäftigen.

Comments

Bin gestern auf diese Aufgabe gestoßen.

Darf ich fragen, in welchem Kontext?

Bin gespannt, wer das lösen kann? hj2166, abakus, der Geo-Freak Roland, ... ??

Im Netz finde ich nur das Umgekehrte:

https://www-user.tu-chemnitz.de/~rhaf/Aufgabensammlung/Einzelaufgabe…

---

Vielleicht geht es mit folgendem Ansatz für eine allgemeine einbeschriebene Ellipse ohne Bedingungen wie bei a) und b) verlangt:

Ellipse: $s(x,y)=ax^2+bx+cy^2+dy+exy+f$

$s_x(x,y)=2ax+b+ey$

$s_y(x,y)=2cy+d+ex$

$s'(x)= -\frac{2ax+b+ey}{2cy+d+ex}$

---

Gelöscht wegen unsinnig.

---

Zeichnung ist im Kommentar.

Punkt P$(p|0)$ liegt auf der Geraden durch A und B mit $m_p=0$

1.)  $ap^2+bp+f=0$

2.)  $0= -\frac{2ap+b}{d+ep}$ 

Punkt Q$(q|4q-12)$ liegt auf der Geraden durch B und C mit $m_q=4$

3.) $aq^2+bq+c(4q-12)^2+d(4q-12)+eq(4q-12)+f=4q-12$

4.)   $4= -\frac{2aq+b+e(4q-12)}{2c(4q-12)+d+eq}$

Punkt R$(r|0,5r)$ liegt auf der Geraden durch C und D mit $m_r=0,5$

5.) $b+\frac{e}{2}r=\frac{1}{2}r$

6.)  $0,5= -\frac{b+\frac{e}{2}r}{2c\frac{e}{2}r+d}$

Punkt S$(0|s)$ liegt auf der senkrechten Geraden  durch A und D  

7.) $cs^2+ds+f=s$

Wolfram war damit überfordert. (Ich auch)

Answer 1

Hallo döschwo,

zunächst mal: vielen Dank für diese Aufgabe und der Kontext der Aufgabe würde mich auch interessieren.

Die Ellipse mit maximalen Flächeninhalt von $A_{\max} \approx 7,46\text{FE}$ sieht etwa so aus:

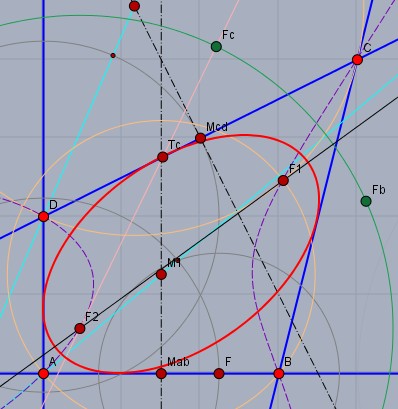
und die mit minimaler Exzentrität von $\epsilon_{\min} \approx 0,616$ sieht so aus:

Die Ergebnisse habe ich zeichnerisch durch Ausmessen gewonnen. Das verwendete Tool ist Cinderella.

Das Vorgehen war wie folgt:

man wähle einen Punkt $F_1$ innerhalb des Vierecks mit der Eigenschaft $$\angle DF_1A + \angle BF_1C = \pi$$dann spiegelt man $F_1$ an den vier Seiten und erhält $F_a$, $F_b$, $F_c$ und $F_d$. Der Mittelpunkt des Kreises (grün), der durch alle vier gespiegelten Punkte verläuft, ist $F_2$ der zweite Brennpunkt der Ellipse. Mit$$|F_2F_c| = 2a, \quad |F_1F_2| = 2e\\ b = \sqrt{a^2-e^2}$$sind die Halbachsen $a$ und $b$ der Ellipse gegeben und daraus lassen sich ihre Exzentrität und Fläche berechnen.

Die lila gestrichelten Kurven sind die Ortslinien, auf denen sich die Brennpunkte $F_{1,2}$ der eingeschriebenen Ellipse befinden können. Dann variiert man die Position von $F_1$ solange bis sich entweder bei $\epsilon$ ein Minimum oder bei $A$ ein Maximum einstellt.

Gruß Werner

Comments

Herzlichen Dank, Werner. Das ist beeindruckend. Ich werde mich erst in ca. 2 Wochen dranmachen können.

Ursprung ist, dass mir jemand dieses Buch nachgeworfen hat, das ich aber erst überflogen habe:

PDF kann ich auf Wunsch ausleihen.

---

noch ein Zusatz:

das Zentrum der Ellipse - also der Mittelpunkt der Strecke $F_1F_2$ liegt für alle eingeschriebenen Ellipsen auf der Geraden$$g: \quad 2x-y=2$$