Berechnen Sie alle Punkte auf der x-Achse, die 9 Einheiten vom Punkt A (1/3/-2) entfernt ist.

Question

Aufgabe:

Berechnen Sie alle Punkte auf der x-Achse, die 9 Einheiten vom Punkt A (1/3/-2) entfernt ist.

Problem/Ansatz:

Vektoren

Comments

Problem/Ansatz:

Vektoren

Eine Entfernung ist kein Vektor.

Den Lösungsweg hat Abakus weiter unten auf dieser Seite aufgeschrieben. Es ist auch gut, sich vorzustellen, dass die Schnittpunkte einer Geraden (der x-Achse) mit einer Kugel (mit Mittelpunkt A und Radius = 9) gesucht sind. Davon kann es maximal zwei geben.

---

Diese Aufgaben (Deine heutigen Fragen) sind alle auf dem gleichen Weg lösbar. Jedesmal dasselbe Muster: Setze die Bedingungen in Gleichungen um, löse diese Gleichungen bzw. das entstehende Gleichungssystem. Vgl Antwort von abakus.

Probier es doch mal selbst.

Answer 1

Ein Punkt auf der x-Achse hat die Koordinaten (x|0|0).

Stelle den Term auf, der den Abstand zwischen den Punkten (1/3/-2) und (x|0|0) beschreibt und setze diesen Term gleich 9.

Löse die entstandene Gleichung nach x auf.

Answer 2

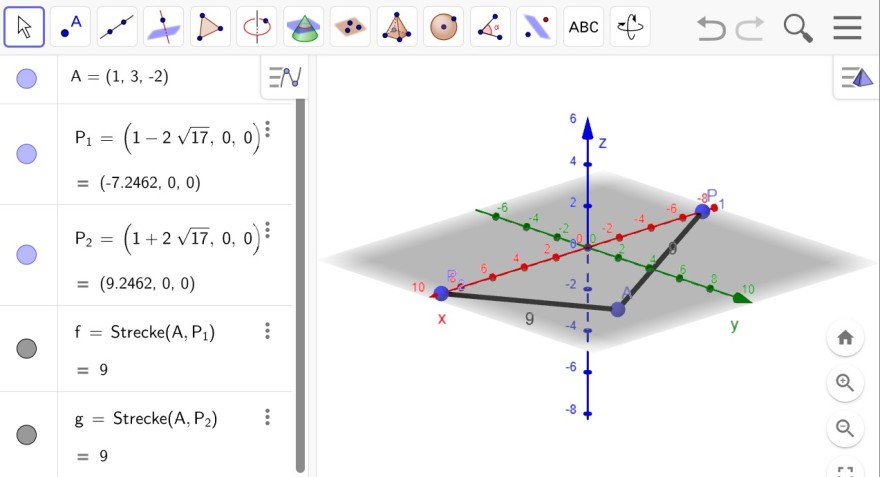
Ein Punkt auf der x-Achse hat den Ortsvektor

P = [x, 0, 0]

Wir bestimmen jetzt den Verbindungsvektor/Richtungsvektor

AP = P - A = [x, 0, 0] - [1, 3, -2] = [x - 1, -3, 2]

Betrag bzw. Länge des Vektors AP muss 9 sein.

|AP| = |[x - 1, -3, 2]| = √(x^2 - 2·x + 1 + 9 + 4) = √(x^2 - 2·x + 14) = 9 --> x = 1 ± 2·√17

Skizze

Comments

Vielen herzlichen Dank