Ein absoluter Hochpunkt ist der höchste Punkt des Graphen (= größter Funktionswert) überhaupt, da kann es also nur einen geben (eine triviale konstante Funktion wie z.B. y=1 schließen wir mal aus). Es ist dafür egal, ob der am Rand oder im Inneren des Definitionsbereiches liegt. Analog ein absolutes Minimum (Tiefpunkt).
Der Begriff ‚Relativer Extremwert‘ bezieht sich auf die Funktionswerte in der Umgebung rechts und links (bei einem Randpunkt natürlich nur auf einer Seite).
An der Stelle x=-3 liegt hier also ein relativer Hochpunkt vor.
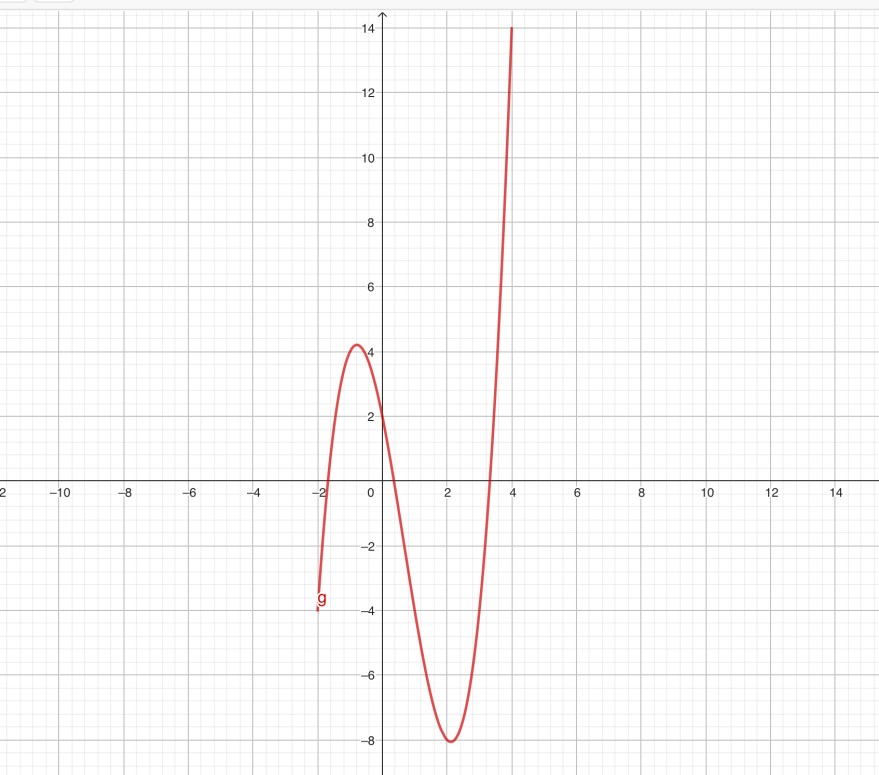
Hier ein Beispiel:absolutes Maximum am Rand bei x=4, absolutes Minimum bei ca. x=2, relatives Maximum bei ca. x=-1 und relatives Minimum am Rand bei x=-2