Nicht ganz korrekt.
Die allgemeine Form wäre übrigens f(x) = a*sin(b*x+d) + c
a: Amplitude (Höhe vom Mittelwert bis Hochpunkt): \( a=\frac{\max -\min }{2} \)
b: Frequenz (wie oft wiederholt sich die Welle?): \( b=\frac{2 \pi}{\text { Periode }} \)
c: Vertikale Verschiebung: \( c=\frac{\max +\min }{2} \)
d: Phase / horizontale Verschiebung: Anhand Verschiebung der Welle z.B. des Hochpunkts
Hier ein Beispiel zum Üben: f(x) = 2sin(π/3*x + π/6) + 2
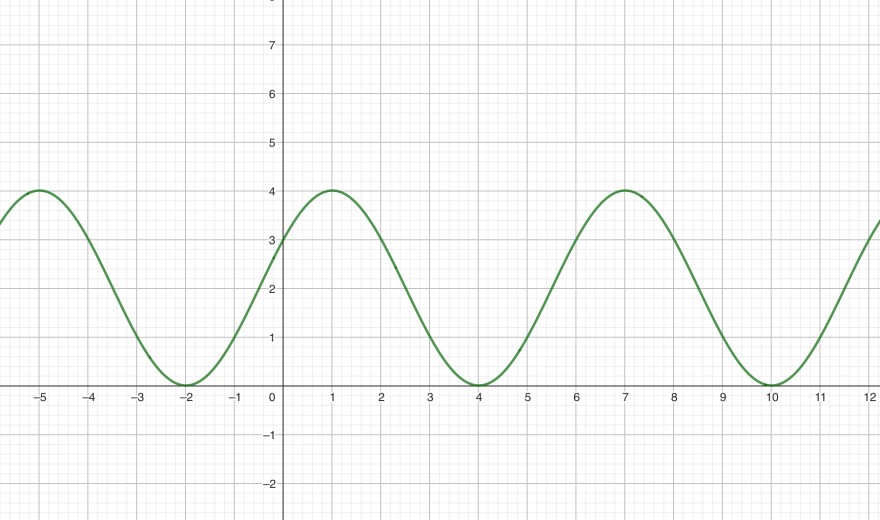
Zur Erklärung:
Periode und Frequenz (Die Periode T ist der Abstand von einem Maximum zum nächsten:
T=6
b=2π/T=2π/6=π/3
Phasenverschiebung (d): Das Maximum einer normalen Sinusfunktion \( (\sin (x)) \) liegt bei \( x=\frac{\pi}{2} \).
Wenn unser Maximum bei \( x=1 \) liegt, dann gilt:
\( b x+d=\frac{\pi}{2} \)
Setze \( x=1, b=\frac{\pi}{3} \) :
\( \frac{\pi}{3} \cdot 1+d=\frac{\pi}{2} \Rightarrow d=\frac{\pi}{2}-\frac{\pi}{3}=\frac{3 \pi-2 \pi}{6}=\frac{\pi}{6} \)