Menge zeichnen im Dreidimensionalen

Question

Aufgabe:

Ich soll diese Menge Zeichnen.

D3 = (x, y, z)^T  ∈ℝ³ I 0 ≤ x ≤ 2 ∧ 0 ≤ y ≤ x ∧ 0 ≤ z ≤ x + y + 1

Problem/Ansatz:

Kann mir einer sagen, wie ich diese Grafik zeichne? Der erste und zweite Teil sind nicht das Problem, wie kann ich das bei geogebra eingeben?

Comments

der erste und zweite teil sind nicht das Problem

Was ist der erste und der zweite Teil?

---

0 ≤ x ≤ 2 ∧ 0 ≤ y ≤ x

also nur der teil mit z der wahrscheinlich dann das Dreieck aufspannt

---

Die Menge ist kein Dreieck, das gibt einen Körper.

Dreieckig sind die Grund- und die Deckfläche.

Die dritte Bedingung begrenzt den sonst in z-Richtung unendlich langen dreikantigen Körper mit einer Grund- und einer Deckfläche. Dabei ist 0 = z die Ebene in der die Grundfläche liegt und z = x + y + 1 die Ebene in der die Deckfläche liegt.

---

wie sieht es den aus oder wie kann ich es bei geogebra eingeben

---

Du könntest die Eckpunkte eingeben und dann verbinden.

Answer 1

Hallo,

ggb kann keine Ungleichungen in 3d darstellen.

Das musst Du mit Surface() modelieren: Ich vereinfache die Einträge nicht damit du die Idee sehen kannst

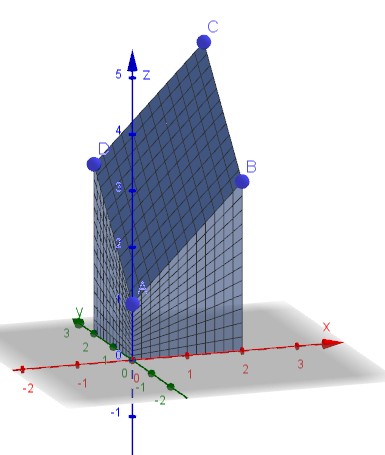
Die Ecken

A=(0,0,1)

B=(2,0,3)

C=(2,2,5)

D=(0,2,3)

Anpassen wenn ich das nicht korrekt gelesen habe...

decke=Surface(u, v, u + v + 1, u, 0, 2, v, 0, 2)

xwand=Surface(A + v (B - A) + u ((2v, 0, 0) - (A + v (B - A))), u, 0, 1, v, 0, 1)

usw....

Comments

Den Punkt D sehe ich nicht, weil dort nicht y ≤ x.

Der Input scheint bei Geogebra mühsam zu sein. In Mathematica habe ich meine Skizze mit einem Einzeiler generiert:

RegionPlot3D[{0 ≤ x ≤ 2 ∧ 0 ≤ y ≤ x ∧ 0 ≤ z ≤ x + y + 1},
{x, 0, 2}, {y, 0, 2}, {z, 0, 5}, PlotPoints -> 100]

aber der Fragesteller hat ja nach Geogebra gefragt.

---

Ja, z.B. 6 Punkte eingeben und verbinden