Aufgabe:
Die folgenden Investitionsvorhaben konkurrieren um die Aufnahme in
das Investitionsprogramm:

a) Als Finanzierungsmaßnahme steht ein Kreditmit einem Volumen
von 680 zu 9% zur Verfügung. Ermitteln Sie graphisch das
Optimalprogramm nach dem Modell von Dean.
Problem/Ansatz:
Ich zeige ab Hier den Rechenweg(Punkt 1-3) und bei Punkt 4 erfolgt die Problemstellung
Legende:
A0 steht für Anfangsauszahlung/Investition
EZÜ steht für Einzahlungsüberschuss
r steht für Restwert.
1. Tabelle um Zeile r ergänzen:
105+105*r=115,5 |-105
105r= 10,5 |:105
r= 1→ 10%
60+60*r=78 |-60
60r=18 |:60
r=0,30 → 30%
240+240*r= 288 |-240
240r = 48 |:240
r= 0,2 → 20%
150+150*r=169,50 |-150
150r =19,50 |:150
r= 0,13 → 13%
320+320*r=340 | -320
320r = 20 |:320
r= 0,06 → 6% ← (IO5) Die Dürfen wir nicht benutzen da in der Aufgabe von 9% die Rede ist, hier würden wir mit 6% ein Verlust fahren.
somit kommen wir auf :

2. Als nächste rechnen wir den % Anteil an Finanziellen Mitteln der genutzt wird. (Hier wird die IO5 weggelassen, weil dieses unter den 9% fällt)
IO1 +IO2 + IO3 + IO4
105+60+240+150 = 555€
555: 680 )*100 = 81,6% Finanzieller Mittel wird genutzt
3. Vermögensendwert bestimmen:
Einzahlungsüberschuss von I01-IO4 = 651€
Investition = 555€
555=*0,9(Zinsen) =49,95
651-555-49,95 = 46,05 Vermögensendwert
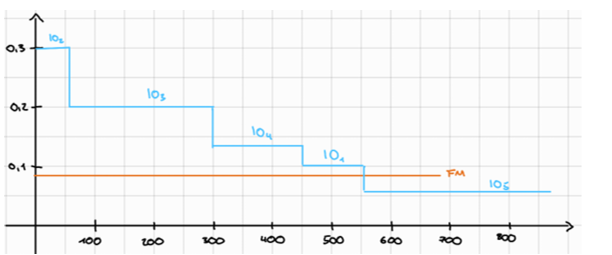
4. Dean Modell zeichnen (Hier befindet sich das Problem)
ich weiß nicht welcher Grenzzinssatz auch genannt cut of point/cut of rate genutzt werden soll.
In der Abbildung habe ich es aus der Aufgabenstellung mit 0,9 gemacht, allerdings habe ich chat gpt gefragt und er meinte, dass die 9% falsch sind. Was könnte hier der Grenzzinsatz sein, diese ist in der Abbildung die Waagerechte Linie.