Hallo Roland,
dass das Viereck \(QRST\) ein Rechteck sein muss, sollte klar sein. Bleibt noch zu zeigen, dass das Verhältnis seiner Seitenlängen gleich \(\Phi = \left(1+\sqrt{5}\right)/2\) ist, also gleich dem 'Goldenen Schnitt'.
Ich betrachte dazu jeweils den Tangens einiger Winkel.
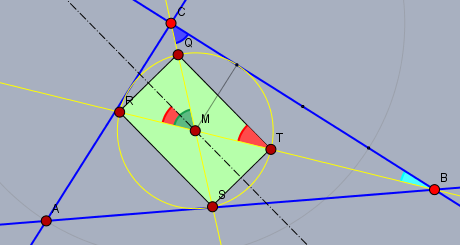
Nach den Halbwinkelformeln ist \(\tan(\beta/2)\) (hellblau)$$\tan\left(\frac{\beta}{2}\right) = \frac{1-\cos(\beta)}{\sin(\beta)} = \frac{1-\frac{4}{5}}{\frac{3}{5}}=\frac{1}{3}$$Der Winkel \(\angle QMR\) (grün) ist$$\angle QMR = \frac{\gamma}{2}+\frac{\beta}{2}$$ Nach den Additionstheoremen ist sein Tangens$$\tan\left(\angle QMR\right) = \tan\left(\frac{\gamma}{2}+\frac{\beta}{2}\right) = \frac{\tan\left(\frac{\gamma}{2}\right)+\tan\left(\frac{\beta}{2}\right)}{1-\tan\left(\frac{\gamma}{2}\right)\tan\left(\frac{\beta}{2}\right)}=\frac{1 + \frac{1}{3}}{1 - \frac{1}{3}}=2$$Und eine weitere Halbwinkelformel liefert den Tangens des halben Winkels \(\angle QTR\) (rot) \(= \angle QMR/2\) und das Verhältnis \(|QT| \div |QR|\)$$\begin{aligned}\frac{|QT|}{|QR|} &= \cot\left(\angle QTR\right) = \frac{1}{\tan\left(\angle QTR\right)} = \frac{1}{\tan\left(\frac{\angle QMR}{2}\right)}\\ &= \frac{1+\sqrt{1+ \tan^2\left(\angle QMR\right)}}{\tan\left(\angle QMR\right)} = \frac{1+\sqrt{1+2^2}}{2} = \Phi\end{aligned}$$
Gruß Werner