Eine geometrische Knobelei

Question

Wie viele Möglichkeiten gibt es, einen Polygonzug aus 13 gleichlangen Teilstrecken zu zeichnen ohne den Stift abzusetzen sowie keine Teilstrecken zweimal zu durchlaufen und dabei vier kongruente Quadrate zu umranden? Kongruente Möglichkeiten sind nicht verschieden.

Comments

Vermutlich geht das nicht?

So ähnlich wie Eulers Brückenproblem.

---

Doch, es geht.

---

willyengland, der Streckenzug muss nicht geschlossen sein.

---

@willengland: Es geht.

[spoiler]

Es gehören 4*4 - 13 = 3 Kanten zu jeweils 2 Quadraten,

[/spoiler]

---

Sehr schön. Gibt es eine weitere Möglichkeit?

---

Hab noch eine aufgezeichnet.

---

Logischer Hintergrund der Aufgabe: 4 Quadrate haben 16 Seiten. Wenn man nur 13 Strecken verwenden soll, müssen 3 der 13 Strecken die gemeinsame Seite von zwei Quadraten sein.

Jetzt muss man nur noch testen, welche der 4 möglichen Lagebeziehungen

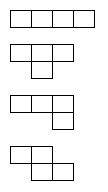
sich in einem Zug zeichnen lassen.

Answer 1

Ok, verstehe, dann geht auch:

Comments

Geht es nicht.

---

Stimmt, 14 Linien.

---

Wie viele Möglichkeiten gibt es

Unendlich viele :

---

So geht es?

...............