Verhältnis von Dreieck / Strahlensatz

Question

Grüße in die Runde

Ich habe folgende Problemstellung und hoffe irgendein Mathegenie hier kann mir helfen.

Gesucht werden der Abstand 42,664 und der Winkel 5,590.
Gegeben sind die beiden Abstände 20,051 und die beiden Winkel 26° und 24°, zusätzlich sind die drei Winkel E1 immer gleich.
Laut meinem CAD ist diese Skizze vollständig definiert was bedeutet die Gesuchten Maße in Klammer ergeben sich durch die gegebenen Werte.

Hat jemand eine Idee wie ich das berechnen könnte?

Vielen Dank

Answer 1

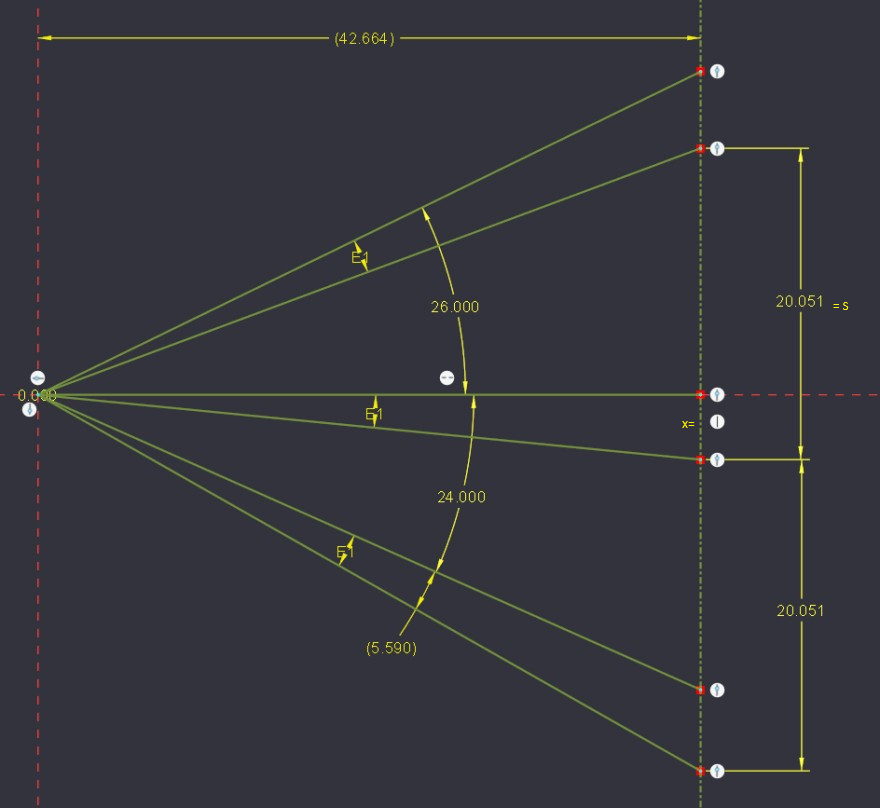
Da sind 3 Tangensbeziehungen in rechtwinkligen Dreiecken.

Setze \(d\) - gesuchte Distanz, \(x\) wie im Bild und \(s=20.051\). Dann gilt

$$s-x=d\tan(26° - E1),\: x=d\tan(E1),\: s+x = d\tan(24°+E1)$$

Auf \(\tan(26° - E1)\) und \(\tan(24°+E1)\) wendest du die Additionsformel für Tanges an.

Wenn du \(t=\tan E1\) setzt, erhältst du ein Gleichungssystem in x,d und t:

Lösung hier.

Der arctan von t gibt dann den gewünschten Winkel.