Statistik Kovarianz und Korrelation

Question

Aufgabe

Text erkannt:

Im Fach F prüfen seit Jahren die Professoren \( X \) und \( Y \), wobei die Studenten „logischerweise" lieber zu \( X \) gehen, weil \( X \) milder sei. In einem Termin haben \( X \) und \( Y \) gemeinsam geprüft, so dass man die von ihnen vergebenen Noten im Einzelnen miteinander vergleichen kann. Es ergab sich folgendes Bild:

\begin{tabular}{|c|c|c|c|c|c|}
\hline Variable & \multicolumn{5}{|c|}{ Variable Y } \\
\cline { 2 - 6 } \( \mathbf{X} \) & \( \mathbf{1} \) & \( \mathbf{2} \) & \( \mathbf{3} \) & \( \mathbf{4} \) & \( \mathbf{5} \) \\
\hline \( \mathbf{1} \) & 1 & 1 & 0 & 0 & 0 \\
\hline \( \mathbf{2} \) & 1 & 2 & 2 & 1 & 0 \\
\hline \( \mathbf{3} \) & 0 & 1 & 2 & 2 & 1 \\
\hline \( \mathbf{4} \) & 0 & 0 & 0 & 1 & 1 \\
\hline
\end{tabular}

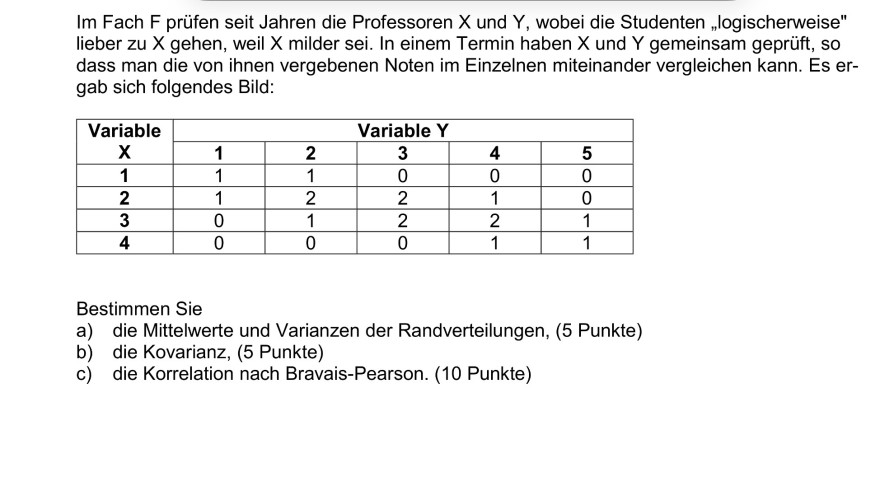
Bestimmen Sie
a) die Mittelwerte und Varianzen der Randverteilungen, (5 Punkte)
b) die Kovarianz, (5 Punkte)
c) die Korrelation nach Bravais-Pearson. (10 Punkte)

Problem/Ansatz:

Mir fehlt komplett der Ansatz da die Variable Y nochmal mit den Noten unterteilt sind.

Answer 1

Mir fehlt komplett der Ansatz da die Variable Y nochmal mit den Noten unterteilt sind.

Daher würde ich zunächst die Werte zu den Rändern aufaddieren.

Wäre damit dein Problem schon gelöst?

Du siehst also, dass 16 Schüler von beiden Professoren bewertet wurden.

Comments

Vielen Dank für die Antwort behindert Kovarianz und der Korrelation tue ich mich noch schwer

---

Meine Ergebnisse zur Kontrolle. Bei Abweichungen kann ich natürlich durchaus auch einen Rechenfehler gemacht haben.

a) μ_x = 2,5 ; s_x^2 = 0,75 ; μ_y = 3 ; s_y^2 = 1,5
b) s_xy = 0,75
c) r = 0,5·√2

---

Alles klar vielen Dank, ich rechne es mal durch und würde mich dann bei Bedarf melden.

Wie lange sind Sie heute erreichbar?

---

Kovarianz

mit dem Verschiebungssatz, kannst du es mit folgender Formel berechnen.

COV(X, Y) = E(X·Y) - E(X)·E(Y)

E steht dabei für den Erwartungswert bzw. hier natürlich für den Mittelwert.

---

Ich komme einfach nicht auf die Kovarianz könntest du mir vielleicht wenn es geht eine ausführliche Lösung zeigen

---

E(X) = 2.5

E(Y) = 3

E(X·Y) = 1·1/16 + 2·1/16 + 3·0/16 + 4·0/16 + 5·0/16 + 2·1/16 + 4·2/16 + 6·2/16 + 8·1/16 + 10·0/16 + 3·0/16 + 6·1/16 + 9·2/16 + 12·2/16 + 15·1/16 + 4·0/16 + 8·0/16 + 12·0/16 + 16·1/16 + 20·1/16 = 33/4 = 8.25

Ich habe für dich das 1/16 mal nicht ausgeklammert, damit du besser sehen kannst, was der Anteil und welcher der Zahlenwert ist, der sich ja aus X·Y ergibt. Ebenso habe ich einen Anteil von 0/16 so stehenlassen, damit du es besser nachvollziehen kannst.

COV(X, Y) = E(X·Y) - E(X)·E(Y)

COV(X, Y) = 8.25 - 2.5·3 = 0.75

---

Super vielen vielen Dank jetzt hab ich es verstanden