Aufgabe Strahlensatz:
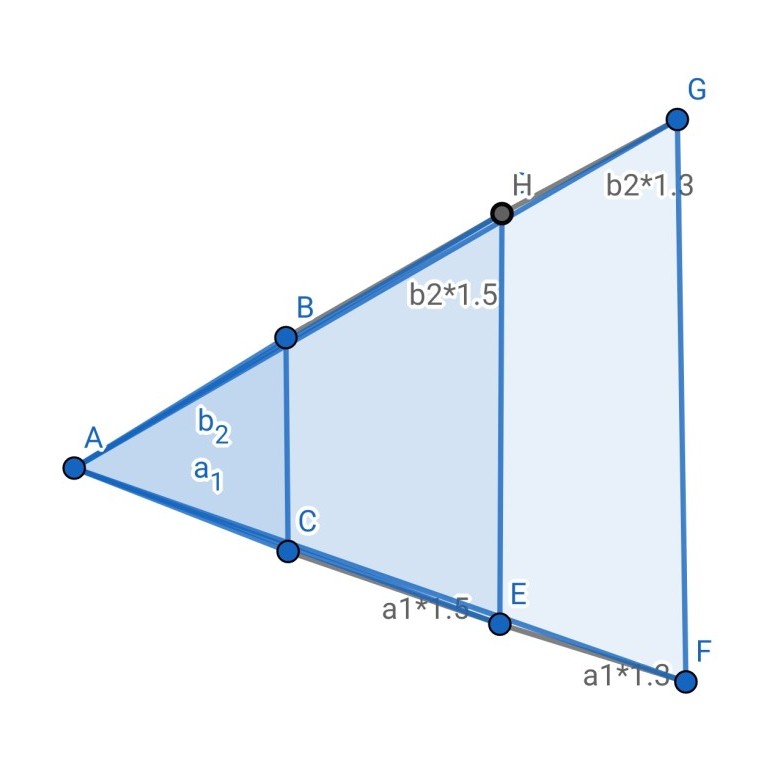
Mich interessiert warum (so habe ich es gelernt jedenfalls) x3/x2 ungleich y3/y2 ist.
In dem Beispiel: (b2*1,3)/(b2*1,5)=/(a1*1,3)/(a1*1,5).
Immerhin sind die sich entsprechenden Seiten immer um den selben Faktor vergrößert. Heisst, wenn x2 um das 2 fache größer ist als x1, muss auch y2 zweifachen so groß sein wie y1. Dann kann ich doch auch y3/y2=x3/x2.
Die Lösung wäre ja dann in meinem Beispiel nach wegstreichen der Faktoren: 1,3/1,5=1,3/1,5