Integralrechnung: Fläche zwischen Graphen bestimmen

Question

Aufgabe:

Gegeben sind die beiden Funktionen f(x) = a - x² und g(x) = x². Bestimme a so, dass die von beiden Graphen eingeschlossene Fläche 9E² beträgt.

Problem/Ansatz:

Ich hoffe jemand kann mir sagen, wie man hier vorgeht. Themengebiet ist Integralrechnung

Comments

Vielleicht hilft ja eine kleine Skizze (hier für a=8):

Kenntnisse von Potenzen/Wurzeln Rechengesetzen sind bei der Aufgabe von Vorteil.

Answer 1

Wo genau drückt der Schuh? Die Fläche zwischen zwei Graphen kann man genauso berechnen, wie die Fläche zwischen dem Graphen der Differenzfunktion \( d(x)=f(x)-g(x) \) und der \( x \)-Achse. Wie das geht, sollte bereits bekannt sein.

Da du weißt, welchen Wert diese Fläche haben soll, kannst du das entsprechende Integral gleich diesen Wert setzen. Das liefert dir dann eine Gleichung für \( a \).

Answer 2

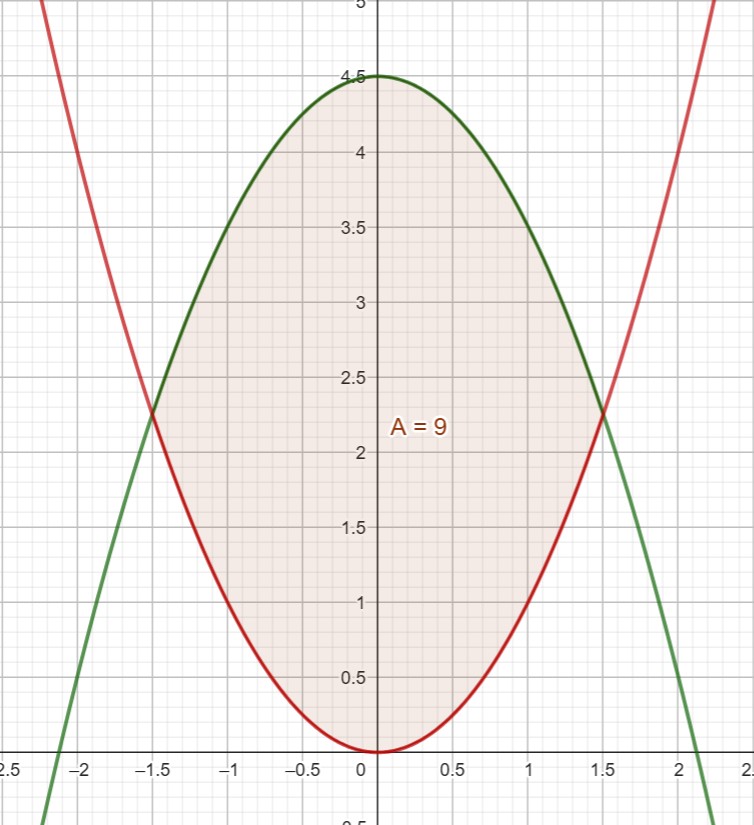
f(x) = a - x² und g(x) = x²

Fläche zwischen zwei Graphen berechnet man oft mit der Differenzfunktion.

d(x) = f(x) - g(x) = a - 2x² = 0 → x = ± √(a/2)

D(x) = a·x - 2/3·x^3 = x·(a - 2/3·x^2)

A = ∫ (- √(a/2) bis √(a/2)) d(x) dx = 2·∫ (0 bis √(a/2)) d(x) dx = 2·D(√(a/2)) = 2·√(a/2)·(a - 2/3·(a/2)) = 2/3·√2·a^(3/2) = 9 → a = 4.5

Skizze mit Geogebra